
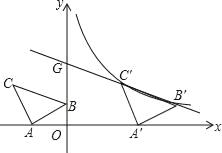
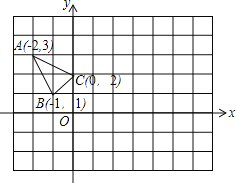
【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(﹣2,0),B(0,1).
(1)求点C的坐标;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B'、C'正好落在某反比例函数图象上.请求出这个反比例函数和此时的直线B'C'的解析式.
(3)若把上一问中的反比例函数记为y1,点B′,C′所在的直线记为y2,请直接写出在第一象限内当y1<y2时x的取值范围.
【答案】(1)C(﹣3,2);(2)y1=![]() , y2=﹣
, y2=﹣![]() x+3; (3)3<x<6.
x+3; (3)3<x<6.
【解析】分析:
(1)过点C作CN⊥x轴于点N,由已知条件证Rt△CAN≌Rt△AOB即可得到AN=BO=1,CN=AO=2,NO=NA+AO=3结合点C在第二象限即可得到点C的坐标;
(2)设△ABC向右平移了c个单位,则结合(1)可得点C′,B′的坐标分别为(﹣3+c,2)、(c,1),再设反比例函数的解析式为y1=![]() ,将点C′,B′的坐标代入所设解析式即可求得c的值,由此即可得到点C′,B′的坐标,这样用待定系数法即可求得两个函数的解析式了;
,将点C′,B′的坐标代入所设解析式即可求得c的值,由此即可得到点C′,B′的坐标,这样用待定系数法即可求得两个函数的解析式了;
(3)结合(2)中所得点C′,B′的坐标和图象即可得到本题所求答案.
详解:
(1)作CN⊥x轴于点N,
∴∠CAN=∠CAB=∠AOB=90°,
∴∠CAN+∠CAN=90°,∠CAN+∠OAB=90°,
∴∠CAN=∠OAB,
∵A(﹣2,0)B(0,1),
∴OB=1,AO=2,
在Rt△CAN和Rt△AOB,
∵ ,
,
∴Rt△CAN≌Rt△AOB(AAS),
∴AN=BO=1,CN=AO=2,NO=NA+AO=3,
又∵点C在第二象限,
∴C(﹣3,2);
(2)设△ABC沿x轴的正方向平移c个单位,则C′(﹣3+c,2),则B′(c,1),
设这个反比例函数的解析式为:y1=![]() ,
,
又点C′和B′在该比例函数图象上,把点C′和B′的坐标分别代入y1=![]() ,得﹣6+2c=c,
,得﹣6+2c=c,
解得c=6,即反比例函数解析式为y1=![]() ,
,
此时C′(3,2),B′(6,1),设直线B′C′的解析式y2=mx+n,
∵![]() ,
,
∴  ,
,
∴直线C′B′的解析式为y2=﹣![]() x+3;
x+3;
(3)由图象可知反比例函数y1和此时的直线B′C′的交点为C′(3,2),B′(6,1),
∴若y1<y2时,则3<x<6.



科目:初中数学 来源: 题型:
【题目】如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
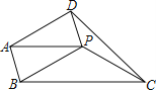
【题目】如图,已知PA=PB=PC=2,∠BPC=120°,PA∥BC.以AB、PB为边作平行四边形ABPD,连接CD,则CD的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
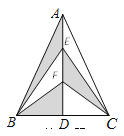
【题目】如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若AD=6cm,CD=3cm,则图中阴影部分的面积是____cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数![]() 的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )
的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
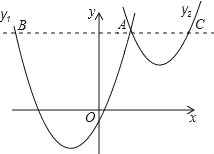
【题目】如图,抛物线y1=a(x+2)2﹣3与y2=![]() (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4;
④2AB=3AC;
其中正确结论是( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.(计算结果精确到0.1m,参考数据sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
(1)当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为 m.
(2)如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.
(1)作△ABC关于点C成中心对称的△A1B1C1,并直接写出A1、B1、C1各点的坐标;
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com