
分析 (1)根据已知得如下规律:
第1个数:4=1×3+1
第2个数:7=2×3+1
第3个数:10=3×3+1
第4个数:13=4×3+1
第5个数:16=5×3+1
第6个数:19=6×3+1
第7个数:22=7×3+1
因此得出第n个数为3n+1
(2)可以利用反证法,首先假设存在这样的三个数和为99,利用连续数之间相差3,可以设出三个数为:m-3、m、m+3,求出m值,再利用第一问求得第n个数的通项公式求得n值为分数.与n为正整数相矛盾,从而证得这列数中,不存在连续三个数的和是99.
解答 (1)解:根据已知4,7,10,13,16,19,22,…
得如下规律:
第1个数:4=1×3+1
第2个数:7=2×3+1
第3个数:10=3×3+1
第4个数:13=4×3+1
第5个数:16=5×3+1
第6个数:19=6×3+1
第7个数:22=7×3+1
…
第n个数:n×3+1
∴第n个数为3n+1
故答案为:3n+1
(2)不存在,
理由如下:
假设在这列数中存在这样的三个数和为99,
设三个数为:m-3、m、m+3,
∴m-3+m+m+3=99
得m=33
令3n+1=33
解得n=$\frac{32}{3}$.
∵n为项数,必须为正整数,
∴n=$\frac{32}{3}$不符合题意,
∴假设不成立
故在这列数中,不存在连续三个数的和是99.
点评 本题考查等差数列的通项公式,本题可以将每个数字分析可以得出他们相同规律为3×n+1,同时也考察反证法.题目第一问较简单,第二问有些难度,可以很好地考查学生的智慧,也体现出数学的概括性和美丽.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
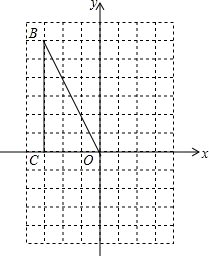 如图,已知O是坐标原点,B(-3,6),C(-3,0),以原点O为位似中心,将△OBC缩小为原来的一半(即新图形与原图形的相似比为1:2).
如图,已知O是坐标原点,B(-3,6),C(-3,0),以原点O为位似中心,将△OBC缩小为原来的一半(即新图形与原图形的相似比为1:2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com