
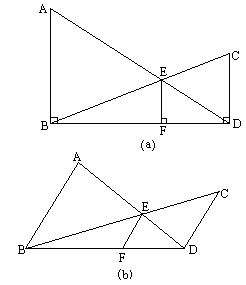
已知:如图(a),AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,可以证明![]() +
+![]() =
=![]() 成立(不要求考生证明).
成立(不要求考生证明).
若将图(a)中的垂直改为斜交,如图(b),AB∥CD,AD、BC相交于点E,过点E作EF∥AB交BD于点F,则
(1)![]() +
+![]() =
=![]() 还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
(2)请找出S△ABD,S△BED和S△BDC间的关系式,并给出证明.
|
证明:如图.
(1)∵AB∥EF,∴ ∵CD∥EF,∴ ∴ ∴ (2)关系式为: 证明如下:分别过A作AM⊥BD于M,过E作EN⊥BD于N,过C作CK⊥BD交BD的延长线于K. 由题设可得: ∴ 即 = 又∵ ∴ |
|
(1)本题告诉我们AB、CD、EF在具备特殊条件(AB⊥BD,CD⊥BD,EF⊥BD)推出平行时,有结论 由条件AB∥EF,CD∥EF,易得出 (2)观察图形可知△ABD、△BED、△BDC是同底(BD边)的三个三角形,只要推出三个三角形在BD边上的关系即可. |


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| 3 |
2
| ||
| 3 |
| 3 |
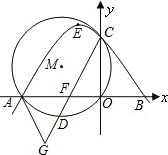 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧 |
| OA |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com