
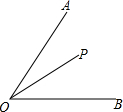
 如图,∠AOB=45°,角内一点P,PO=10,两边上各有点Q,R(均不同于O),则△PQR的周长的最小值为
如图,∠AOB=45°,角内一点P,PO=10,两边上各有点Q,R(均不同于O),则△PQR的周长的最小值为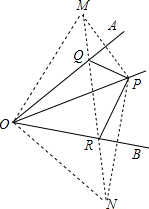
| 102+102 |
| 2 |
| 2 |


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
 如图,在宽为30m,长为40m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.根据图中数据,计算耕地的面积为( )
如图,在宽为30m,长为40m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.根据图中数据,计算耕地的面积为( )| A、1200m2 |
| B、1131m2 |
| C、1181 m2 |
| D、1209m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
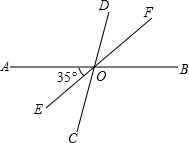 直线AB,CD相交于O,过点O画射线OE,OF,已知∠AOE=35°,∠EOC=∠DOF
直线AB,CD相交于O,过点O画射线OE,OF,已知∠AOE=35°,∠EOC=∠DOF查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com