
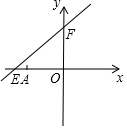
 如图,直线y=kx+6与x轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).
如图,直线y=kx+6与x轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).分析 (1)由E点坐标代入可求得k的值;
(2)由P点坐标可表示出P到x轴的距离,则可表示出S与x之间的函数关系式,由P在第二象限可求得x的取值范围;
(3)由三角形OPA的面积OA•|yP|=9可求得P点纵坐标,即可求得P点的位置.
解答 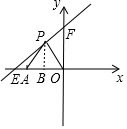 解:
解:
∵直线y=kx+6与x轴分别交于E、F.点E坐标为(-8,0),
∴0=-8k+6,解得k=$\frac{3}{4}$;
(2)如图,过P作PB⊥x轴于点B,
∵k=$\frac{3}{4}$,
∴直线解析式为y=$\frac{3}{4}$x+6,
∵P(x,y)是第二象限内的直线上的一个动点,
∴y=$\frac{3}{4}$x+6,
∴PB=$\frac{3}{4}$x+6,
∵A(-6,0),
∴OA=6,
∴S=$\frac{1}{2}$OA•PB=$\frac{1}{2}$×6($\frac{3}{4}$x+6)=$\frac{9}{4}$x+18,
∵点P在第二象限,
∴点B在线段OA上,
∵A(-8,0),
∴-8<x<0,
∴S与x的函数关系式为S=$\frac{9}{4}$x+18(-8<x<0);
(3)∵S△OPA=$\frac{1}{2}$OA•|yP|=9,P(x,y),
∴$\frac{1}{2}$×6×|y|=9,解得y=3或-3,
当y=3时,代入y=$\frac{3}{4}$x+6中得,$\frac{3}{4}$x+6=3,
∴x=-4,
∴P点坐标为(-4,3);
当y=-3时,代入y=$\frac{3}{4}$x+6中得,$\frac{3}{4}$x+6=-3,
∴x=-12,
∴P点坐标为(-12,-3);
综上可知,当P点运动到(-4,3)或(-12,-3)处,三角形OPA的面积为9.
点评 本题为一次函数的综合应用,涉及待定系数法、函数图象上点的坐标特征、三角形的面积等知识.在(1)中注意利用函数图象点的点的坐标满足函数解析式可得到关于k的方程,在(2)中用x表示出P到x轴的距离是解题的关键,在(3)中求得P点的纵坐标是解题的关键,注意分两种情况.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:填空题
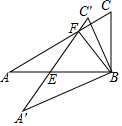 如图,△ABC≌△A′BC′,∠ABC=90°,∠A′=30°.(0°<∠ABA′≤60°),A′C′与AC交于点F,与AB交于点E,连接BF.当△BEF为等腰三角形时,则∠AB A′的角度为20°或40°.
如图,△ABC≌△A′BC′,∠ABC=90°,∠A′=30°.(0°<∠ABA′≤60°),A′C′与AC交于点F,与AB交于点E,连接BF.当△BEF为等腰三角形时,则∠AB A′的角度为20°或40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
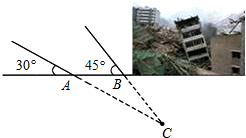 如图,某煤矿因不按规定操作发生瓦斯爆炸,救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A,B两个探测点探测到地下C处有生命迹象.已知A,B两点相距8米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度(结果保留根号).
如图,某煤矿因不按规定操作发生瓦斯爆炸,救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A,B两个探测点探测到地下C处有生命迹象.已知A,B两点相距8米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
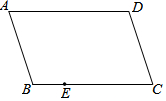 如图,ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.画出满足题意的点F,并简要说明你的画图过程.
如图,ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.画出满足题意的点F,并简要说明你的画图过程.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | -3 | -2 | -1 | 1 | 2 | 3 |
| y=-x+1 | 4 | 3 | 2 | 0 | -1 | -2 |
| y=$\frac{k}{x}$ | $\frac{2}{3}$ | 1 | 2 | -2 | -1 | -$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
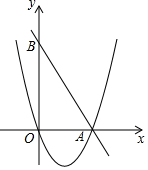 在平面直角坐标系xOy中,抛物线y=ax2-2ax交x轴于O、A两点,过点A的直线y=-$\frac{4}{7}$ax+b交y轴于点B,AB=2$\sqrt{5}$.
在平面直角坐标系xOy中,抛物线y=ax2-2ax交x轴于O、A两点,过点A的直线y=-$\frac{4}{7}$ax+b交y轴于点B,AB=2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com