
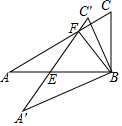
 如图,△ABC≌△A′BC′,∠ABC=90°,∠A′=30°.(0°<∠ABA′≤60°),A′C′与AC交于点F,与AB交于点E,连接BF.当△BEF为等腰三角形时,则∠AB A′的角度为20°或40°.
如图,△ABC≌△A′BC′,∠ABC=90°,∠A′=30°.(0°<∠ABA′≤60°),A′C′与AC交于点F,与AB交于点E,连接BF.当△BEF为等腰三角形时,则∠AB A′的角度为20°或40°. 分析 根据0°<∠ABA′≤60°,分两种情况进行讨论:当FE=FB时,△BEF为等腰三角形;当BE=FB时,△BEF为等腰三角形,根据全等三角形对应边上的高相等,可得BP=BQ,进而得到∠PFB=∠QFB,再根据三角形外角性质以及三角形内角和定理,即可得到∠FEB的度数,最后根据三角形外角性质即可得出∠ABA′的角度.
解答 解:如图,当FE=FB时,△BEF为等腰三角形,设∠FEB=∠FBE=α,
过B作BP⊥AC,BQ⊥A'C',由全等三角形对应边上的高相等,可得BP=BQ,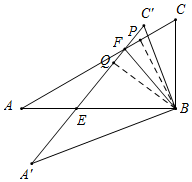
∴点B在∠PFQ的角平分线上,
∴∠PFB=∠QFB,
∵∠PFB是△ABF的外角,
∴∠PFB=∠A+∠FBE=30°+α,
∴∠QFB=30°+α,
∵△BEF中,∠QFB+∠FEB+∠FBE=180°,
∴30°+α+2α=180°,
解得α=50°,
∴∠ABA'=∠FEB-∠A'=50°-30°=20°;
如图,当BE=BF时,△BEF为等腰三角形,设∠FEB=∠BFE=α,
过B作BP⊥AC,BQ⊥A'C',由全等三角形对应边上的高相等,可得BP=BQ,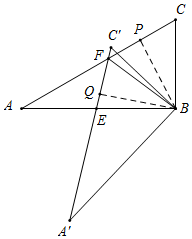
∴点B在∠PFQ的角平分线上,
∴∠PFB=∠QFB=α,
∵∠PFB是△ABF的外角,
∴∠FBE=∠PFB-∠A=α-30°,
∵△BEF中,∠QFB+∠FEB+∠FBE=180°,
∴α+α+α-30°=180°,
解得α=70°,
∴∠ABA'=∠FEB-∠A'=70°-30°=40°;
综上所述,∠ABA′的角度为20°或40°.
故答案为:20°或40°.
点评 本题主要考查了全等三角形的性质,三角形外角性质以及三角形内角和定理的综合应用,解决问题的关键是依据全等三角形对应边上的高相等,得出BP=BQ,进而得到点B在∠PFQ的角平分线上.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学校开展阳光体育活动,组织九年级学生定点投篮,规定每人投篮3次.现对九年级(5)班每名学生投中篮的次数进行统计,并将统计结果绘制成如下不完整的统计图表.
学校开展阳光体育活动,组织九年级学生定点投篮,规定每人投篮3次.现对九年级(5)班每名学生投中篮的次数进行统计,并将统计结果绘制成如下不完整的统计图表. | 投中篮的次数(次) | 频数 (人数) | 频率 |
| 0 | 2 | 0.05 |
| 1 | 12 | 0.3 |
| 2 | x | 0.45 |
| 3 | 8 | y |
| 合计 | m | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
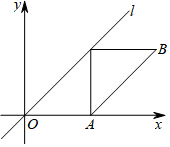 如图,在平面直角坐标系中,已知点A($\frac{3}{2}$$\sqrt{2}$,0),点B在第一象限,且AB与直线l:y=x平行,AB长为4,若点P是直线l上的动点,则△PAB的内切圆面积的最大值为$\frac{1}{4}$π.
如图,在平面直角坐标系中,已知点A($\frac{3}{2}$$\sqrt{2}$,0),点B在第一象限,且AB与直线l:y=x平行,AB长为4,若点P是直线l上的动点,则△PAB的内切圆面积的最大值为$\frac{1}{4}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
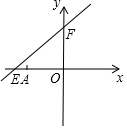 如图,直线y=kx+6与x轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).
如图,直线y=kx+6与x轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com