
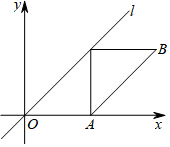
 如图,在平面直角坐标系中,已知点A($\frac{3}{2}$$\sqrt{2}$,0),点B在第一象限,且AB与直线l:y=x平行,AB长为4,若点P是直线l上的动点,则△PAB的内切圆面积的最大值为$\frac{1}{4}$π.
如图,在平面直角坐标系中,已知点A($\frac{3}{2}$$\sqrt{2}$,0),点B在第一象限,且AB与直线l:y=x平行,AB长为4,若点P是直线l上的动点,则△PAB的内切圆面积的最大值为$\frac{1}{4}$π. 分析 根据AB=4以及直线l和点A的位置,求出△ABP的面积,利用三角形与内切圆关系是:r=(2×三角形面积)÷三角形周长(a+b+4),再根据a+b>4找r的最大值后求得最大面积即可.
解答 解:作点A关于直线l的对称点A′,连接AA′交直线l于点C,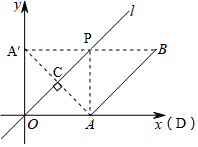
由直线y=x中k=1可知∠COA=45°,
在Rt△AOC中,OC=AC=OAcos∠AOC=$\frac{3\sqrt{2}}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{3}{2}$,
则AA′=2AC=3,
∵AB∥直线l,
∴∠BAD=45°,
∴∠BAA′=90°,
连接A′B交直线l于点P,连接PA,
则此时△PAB的周长最小,S△PAB=$\frac{1}{2}$×4×$\frac{3}{2}$=3,
在Rt△AA′B中,A′B=$\sqrt{AA{′}^{2}+A{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴△PAB周长的最小值为3+4+5=12,
由三角形内切圆的半径r=$\frac{2S}{a+b+c}$知,三角形的周长最小时,三角形内切圆的半径最大,最大半径r=$\frac{2×3}{12}$=$\frac{1}{2}$,
∴△PAB的内切圆面积的最大值为$\frac{1}{4}$π,
故答案为:$\frac{1}{4}$π.
点评 本题考查了两直线相交或平行问题及三角形的内切圆的半径与三边和面积之间的关系,掌握三角形内切圆半径与周长和面积之间的关系是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图:已知线段a、b
如图:已知线段a、b查看答案和解析>>
科目:初中数学 来源: 题型:填空题
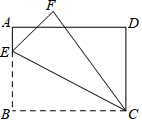 如图,矩形ABCD中,AB=4,BC=6,E为AB上一点,将△BCE沿CE翻折至△FCE,EF与AD相交于点G,且AG=FG,则线段AE的长为1.
如图,矩形ABCD中,AB=4,BC=6,E为AB上一点,将△BCE沿CE翻折至△FCE,EF与AD相交于点G,且AG=FG,则线段AE的长为1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
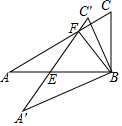 如图,△ABC≌△A′BC′,∠ABC=90°,∠A′=30°.(0°<∠ABA′≤60°),A′C′与AC交于点F,与AB交于点E,连接BF.当△BEF为等腰三角形时,则∠AB A′的角度为20°或40°.
如图,△ABC≌△A′BC′,∠ABC=90°,∠A′=30°.(0°<∠ABA′≤60°),A′C′与AC交于点F,与AB交于点E,连接BF.当△BEF为等腰三角形时,则∠AB A′的角度为20°或40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
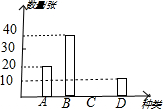 假期,某学校组织学生分别到A、B,C、D四个地方进行研习旅行,学校按定额购买了前往四地的车票,如图是未制作完成的车票种类和数量的条形统计图,请根据统计图回答下列问题:
假期,某学校组织学生分别到A、B,C、D四个地方进行研习旅行,学校按定额购买了前往四地的车票,如图是未制作完成的车票种类和数量的条形统计图,请根据统计图回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
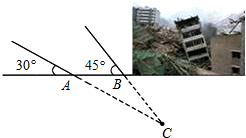 如图,某煤矿因不按规定操作发生瓦斯爆炸,救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A,B两个探测点探测到地下C处有生命迹象.已知A,B两点相距8米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度(结果保留根号).
如图,某煤矿因不按规定操作发生瓦斯爆炸,救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A,B两个探测点探测到地下C处有生命迹象.已知A,B两点相距8米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com