
【题目】在△ABC中,BD为∠ABC的平分线.
(1)如图1,∠C=2∠DBC,∠A=60°,求证:△ABC为等边三角形;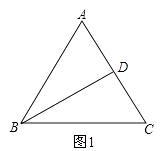
(2)如图2,若∠A=2∠C,BC=8,AB=4.8,求AD的长度;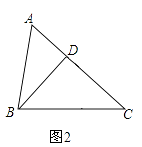
(3)如图3,若∠ABC=2∠ACB,∠ACB的平分线OC与BD相交于点O,且OC=AB,求∠A的度数.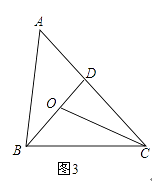
【答案】
(1)
解:∵BD为∠ABC的平分线,
∴∠ABC=2∠DBC
∵∠C=2∠DBC,
∴∠ABC=∠C,
∴AB=AC,
∵∠A=60°,
∴△ABC是等边三角形
(2)
解:如图2,截取BE=AB,连接DE,

在△ABD与△EBD中, 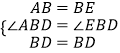 ,
,
∴△ABD≌△EBD,
∴∠A=∠DEB,AD=ED,
∵∠A=2∠C,
∴∠DEB=2∠C,
∵∠DEB=∠C=∠EDB,
∴∠C+∠EDB=2∠C,
∴∠C=∠EDB,
∴ED=EC,
∵AB=4.8,
∴CE=BC﹣BE=3.2,
∴AD=DE=CE=3.2
(3)
解:如图3,过B作BF平分∠DBC交AC于F,

∵BD平分∠ABC,
∴∠ABD=∠CBD= ![]() ∠ABC,
∠ABC,
即∠ABC=2∠ABD=2∠CBD,
∵∠ABC=2∠ACB,
∴∠ACB=∠ABD=∠CBD,
∵OC平分∠ACB,BF平分∠DBC,
∴∠1=∠3= ![]() ∠DBC,∠4=∠2=
∠DBC,∠4=∠2= ![]() ∠ACB,
∠ACB,
∴∠1=∠2=∠3=∠4,
在△OBC与△FCB中,  ,
,
∴△OBC≌△FCB,
∴OC=BF,
∵AB=OC,
∴BF=AB,
∵∠ABF=∠ABD+∠3,∠AFB=∠ACB+∠1,
∵∠ABD=∠ACB,∠1=∠3,
∴∠ABF=∠AFB,
∴AB=AF,
∴AB=BF=AF,
∴△ABF为等边三角形,
∴∠A=60°
【解析】(1)由BD为∠ABC的平分线,得到∠ABC=2∠DBC,等量代换得到∠ABC=∠C,证得AB=AC,即可得到结论;(2)如图2,截取BE=AB,连接DE,推出△ABD≌△EBD,根据全等三角形的性质得到∠A=∠DEB,AD=ED,由∠A=2∠C,得到∠DEB=2∠C,求出∠C=∠EDB,得到ED=EC即可得到结论;(3)过B作BF平分∠DBC交AC于F,根据角平分线的性质得到BD平分∠ABC,∠ABC=2∠ABD=2∠CBD,由∠ABC=2∠ACB,得到∠ACB=∠ABD=∠CBD,由角平分线的定义得到∠1=∠3= ![]() ∠DBC,∠4=∠2=
∠DBC,∠4=∠2= ![]() ∠ACB,推出△OBC≌△FCB,根据全等三角形的性质得到OC=BF,由AB=OC,得到BF=AB等量代换得到∠ABF=∠AFB,求得AB=AF,即可得到结论.
∠ACB,推出△OBC≌△FCB,根据全等三角形的性质得到OC=BF,由AB=OC,得到BF=AB等量代换得到∠ABF=∠AFB,求得AB=AF,即可得到结论.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对角平分线的性质定理的理解,了解定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=60°,BD,CD分别平分∠ABC,∠ACB,M,N,Q分别在DB,DC,BC的延长线上,BE,CE分别平分∠MBC,∠BCN,BF,CF分别平分∠EBC,∠ECQ,则∠F= . 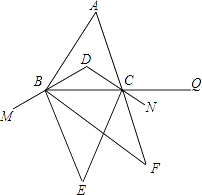
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如图①,在![]() 中,试说明
中,试说明![]() .
.
分析:通过画平行线,将![]() 、
、![]() 、
、![]() 作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法.
作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法.
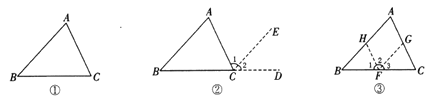
解:如图②,延长![]() 到点
到点![]() ,过点
,过点![]() 作
作![]() //
//![]() .
.
因为![]() //
//![]() (作图所知),
(作图所知),
所以![]() ,
,![]() (两直线平行,同位角、内错角相等).
(两直线平行,同位角、内错角相等).
又因为![]() (平角的定义),
(平角的定义),
所以![]() (等量代换).
(等量代换).
如图③,过![]() 上任一点
上任一点![]() ,作
,作![]() //
//![]() ,
, ![]() //
//![]() ,这种添加辅助线的方法能说
,这种添加辅助线的方法能说![]() 吗?并说明理由.
吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小明玩数学游戏,小丽取出一个不透明的口袋,口袋中装有四张分别标有数字2,3,4,6的卡片,卡片除数字外其余都相同,小丽要求小明从中随机抽取一张卡片并记录下卡片上的数字,将卡片放回洗匀,再次从中随机抽取一张卡片,同样记录下卡片上的数字.
(1)请用画树状图或列表的方法表示小明两次抽取卡片的所有可能出现的结果;
(2)求小明抽到的两张卡片上的数都能被2整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
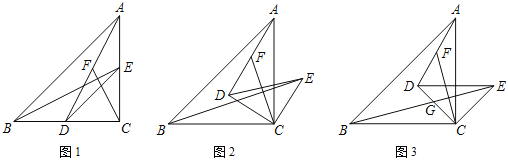
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,D,E分别为AC,BC上的点,且CE=CD,连接DE,AD,BE,F为线段AD的中点,连接CF.
(1)求证:BE=2CF;
(2)如图2,把△DEC绕点C顺时针旋转α角(0°<α<90°),其他条件不变,试探究线段BE与CF的位置关系,并说明理由;
(3)如图3,把△DEC绕点C顺时针旋转45°,BE,CD交于点G.若∠DCF=30°,求![]() 及
及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面去括号正确的是( )
A. a﹣(b+1)=a﹣b﹣1B. 2(x+3)=2x+3
C. x﹣(y﹣1)=x﹣y﹣1D. ﹣3(m﹣n)=﹣3m﹣3n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断错误的是( )
A.有两组邻边相等的四边形是菱形B.有一角为直角的平行四边形是矩形
C.对角线互相垂直且相等的平行四边形是正方形D.矩形的对角线互相平分且相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com