
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
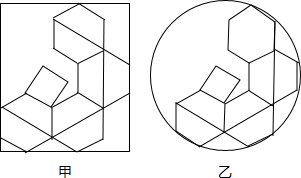
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
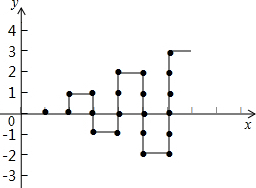
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
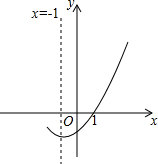 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:| A. | ①② | B. | ②④ | C. | ①③ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,它与x轴的一个交点是(-1,0).则抛物线与x轴的另一个交点是(5,0);a+b+c<0(填“<或=或>”)
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,它与x轴的一个交点是(-1,0).则抛物线与x轴的另一个交点是(5,0);a+b+c<0(填“<或=或>”)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
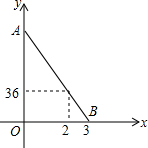 小王骑车从甲地到乙地,小李骑车从乙地到甲地,两人同时出发,沿同一条公路匀速前进,在出发2h时,两人相距36km,在出发3h时,两人相遇.设骑行的时间为x(h),两人之间的距离为y(km),图中的线段AB表示两人从出发到相遇这个过程中,y与x之间的函数关系.
小王骑车从甲地到乙地,小李骑车从乙地到甲地,两人同时出发,沿同一条公路匀速前进,在出发2h时,两人相距36km,在出发3h时,两人相遇.设骑行的时间为x(h),两人之间的距离为y(km),图中的线段AB表示两人从出发到相遇这个过程中,y与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com