解:(1)∵y=ax
2-4ax+c=a(x-2)
2-4a+c,
∴抛物线的对称轴为直线x=2.
∵点D(4,-3)在抛物线上,∴由对称性知C(0,-3).
∴四边形ABCD为梯形.
由四边形ABDC的面积为18、CD=4,OC=3得AB=8,∴A(-2,0).
由A(-2,0)、C(0,-3)得y=

x
2-x-3.
(2)∵S
四边形ABDC=18,S
△OBD=9,
∴S
△OBD=

S
四边形ABDC,
∴只可能出现两种情形:
①直线y=kx与边BD相交于点E,且S
△OBE=

S
四边形ABDC=

×18=6;
∵OB=6,
∴点E到OB的距离为2,
直线BD的解析式为y=

x-9,
令y=-2,则x=

,
∴E点坐标为(

,-2)
把E(

,-2)代入y=kx得k=-

;
②直线y=kx与边CD相交于点F,且S
四边形OBDF=

S
四边形ABDC=

×18=12;

∵OB=6,
∴DF=2,
∴F点坐标为(2,-3),
把F(2,-3)代入y=kx得k=-

.
(3)翻折后点C′(0,3),由图形的位似及相似比为2,可得:
∵根据位似得平行k相等设解析式,
直线AC′的解析式为:y=kx+b,
∴
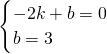
,
解得:

,
∴y=1.5x+3,
∴直线EG的解析式为:y=1.5x+c,
∴两函数交点坐标为:

,
∴整理可得出:x
2-10x-12-4c=0,
∴x
1+x
2=10,
∵图形的位似及相似比为2,
∴EN=2AO=4,GN=2C′O=6,
∴x
2-x
1=4,
解得:x
2=7,x
1=3,
∴E点横坐标为:3,进而得出纵坐标为:-

,
或E点横坐标为:7,进而得出纵坐标为:

,
即可得出:
①若为同向放大,则E(3,-

)、G(7,

);
②若为反向放大,则E(7,

)、G(3,-

).
若为情形①,则P(-7,

);
若为情形②,
则P(1,

).
分析:(1)由抛物线解析式可知抛物线对称轴为x=2,根据对称性可求C点坐标,则四边形ABDC为等腰梯形,CD=4,OC=3,由已知四边形面积可求AB=8,根据等腰梯形的性质可求A点坐标,将A、C两点坐标代入抛物线解析式即可;
(2)由(1)可知S
四边形ABDC=18,S
△OBD=9,则S
△OBD=

S
四边形ABDC,分①直线y=kx与边BD相交,②直线y=kx与边CD相交,两种情况求k的值;
(3)存在.翻折后点C′(0,3),由图形的位似及相似比为2,按照①同向放大,②反向放大,两种情况,根据C′为PG的中点,由相似比求P、E、G的坐标.
点评:本题考查了二次函数的综合运用.关键是根据抛物线的对称性,判断四边形ABDC为等腰梯形,求顶点坐标,确定抛物线解析式,再根据面积关系确定P点坐标.

 线上,且四边形ABDC的面积为18.
线上,且四边形ABDC的面积为18. x2-x-3.
x2-x-3. S四边形ABDC,
S四边形ABDC, S四边形ABDC=
S四边形ABDC= ×18=6;
×18=6; x-9,
x-9, ,
, ,-2)
,-2) ,-2)代入y=kx得k=-
,-2)代入y=kx得k=- ;
; S四边形ABDC=
S四边形ABDC= ×18=12;
×18=12;
 .
.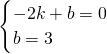 ,
, ,
, ,
, ,
, ,
, )、G(7,
)、G(7, );
); )、G(3,-
)、G(3,- ).
). );
); ).
). S四边形ABDC,分①直线y=kx与边BD相交,②直线y=kx与边CD相交,两种情况求k的值;
S四边形ABDC,分①直线y=kx与边BD相交,②直线y=kx与边CD相交,两种情况求k的值;

 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).