
【题目】如图,平行四边形![]() 中,
中,![]() ,
,![]() ,∠
,∠![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 的边上,若
的边上,若![]() 为等腰三角形,则
为等腰三角形,则![]() 的长为__________.
的长为__________.

【答案】![]() 或
或![]() 或6
或6
【解析】
根据点P所在的线段分类讨论,再分析每种情况下![]() 腰的情况,然后利用直角三角形的性质和勾股定理分别求值即可.
腰的情况,然后利用直角三角形的性质和勾股定理分别求值即可.
解:①当点P在AB上时,由∠ABC=120°,此时![]() 只能是以∠PBE为顶角的等腰三角形,BP=BE,过点B作BF⊥PE于点F,如下图所示
只能是以∠PBE为顶角的等腰三角形,BP=BE,过点B作BF⊥PE于点F,如下图所示

∴∠FBE=![]() ∠ABC=60°,EP=2EF
∠ABC=60°,EP=2EF
∴∠BEF=90°-∠FBE=30°
∵![]() ,点
,点![]() 是
是![]() 的中点
的中点
∴BE=![]()
在Rt△BEF中,BF=![]()
根据勾股定理:EF=![]()
∴EP=2EF=![]() ;
;
②当点P在AD上时,过点B作BF⊥AB于F,过点P作PG⊥BC,如下图所示
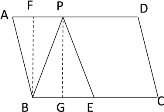
∵∠ABC=120°
∴∠A=60°
∴∠ABF=90°-∠A=30°
在Rt△ABF中AF=![]() ,BF=
,BF=![]()
∴BP≥BF>BE,EP≥BF>BE
∴此时![]() 只能是以∠BPE为顶角的等腰三角形,BP=PE,
只能是以∠BPE为顶角的等腰三角形,BP=PE,
∴PG=BF=![]() ,EG=
,EG=![]()
根据勾股定理:EP=![]() ;
;
③当点P在CD上时,过点E作EF⊥CD于F,过点B作BG⊥CD

由②可知:BE的中垂线与CD无交点,
∴此时BP≠PE
∵∠A=60°,四边形ABCD为平行四边形
∴∠C=60°
在Rt△BCG中,∠CBG=90°-∠C=30°,CG=![]()
根据勾股定理:BG=![]()
∴BP≥BG>BE
∵EF⊥CD,BG⊥CD,点E为BC的中点
∴EF为△BCG的中位线
∴EF=![]()
∴此时![]() 只能是以∠BEP为顶角的等腰三角形,BE=PE=6.
只能是以∠BEP为顶角的等腰三角形,BE=PE=6.
综上所述:![]() 的长为
的长为![]() 或
或![]() 或6.
或6.
故答案为:![]() 或
或![]() 或6
或6


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
(1)求证:四边形BCFE是菱形;
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在对Rt△OAB依次进行位似、轴对称和平移变换后得到△O′A′B′.
(1)在坐标纸上画出这几次变换相应的图形;
(2)设P(x,y)为△OAB边上任一点,依次写出这几次变换后点P对应点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2013的坐标为

A. (2,1006)B. (1008,0)C. ( -1006,0)D. (1,-1007)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】贺岁片《流浪地球》被称为开启了中国科幻片的大门,2019也被称为中国科幻片的元年.某电影院为了全面了解观众对《流浪地球》的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).根据以上信息,解答下列问题:
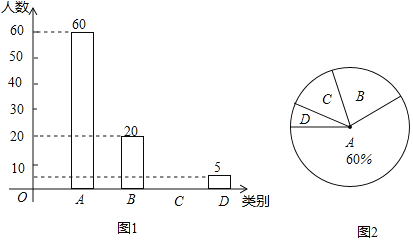
(1)本次接受调查的观众共有 人;
(2)扇形统计图中,扇形C的圆心角度数是 .
(3)请补全条形统计图;
(4)春节期间,该电影院来观看《流浪地球》的观众约3000人,请估计观众中对该电影满意(A、B、C类视为满意)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=-x+(k+13)和反比例函数![]() 的图象相交于点A与点B.过A点作AC⊥x轴于点C,S△AOC=6.
的图象相交于点A与点B.过A点作AC⊥x轴于点C,S△AOC=6.

(1)求反比例函数和一次函数的解析式;
(2)求点A与点B的坐标;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作ECFG.
(1)如图1,证明ECFG为菱形;
(2)如图2,若∠ABC=120°,连接BG、CG,并求出∠BDG的度数:
(3)如图3,若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王平同学为小明与小丽设计了一种游戏.游戏规则是:取3张数字分别是2、3、4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再按原样放回,洗匀后第二次再随机抽出一张牌记下数字,若抽出的两张牌上的数字之和为偶数,则小明胜;若两数字之和为奇数,则小丽胜.问这种游戏规则公平吗?请通过画树状图或列表说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com