【题目】如图，一次函数y=-x+（k+13）和反比例函数
的图象相交于点A与点B.过A点作AC⊥x轴于点C，S△AOC=6.
（1）求反比例函数和一次函数的解析式；
（2）求点A与点B的坐标；
（3）求△AOB的面积.
口算题卡北京妇女儿童出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，港口B位于港口A的南偏东
方向，灯塔C恰好在AB的中点处，一艘海轮位于港口A的正南方向，港口B的正西方向的D处，它沿正北方向航行
km，到达E处，测得灯塔C在北偏东
方向上．这时，E处距离港口A有多远？（参考数据： 
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在菱形ABCD中，AB=BD，点E、F分别在BC、CD上，且BE=CF，连接BF、DE交于点M，延长ED到H使DH=BM，连接AM，AH，则以下四个结论：
①△BDF≌△DCE；②∠BMD=120°；③△AMH是等边三角形；④S四边形ABCD= 
AM2．
其中正确结论的个数是（ ）
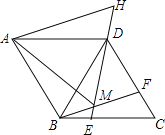
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．
（1）观察猜想
如图1，当点D在线段BC上时，
① BC与CF的位置关系为 ；
② BC，CD，CF之间的数量关系为 ．（直接写出结论）
（2）数学思考
如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．
（3）拓展延伸
如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=
， CD=
BC，则GE的长为 ．（请直接写出结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知正方形
，
为边
上一点
不与
、
重合），过作
，且
，连接
．
（1）如图1，求
的度数；
（2）如图2，连接
交
于
，求证：
；
（3）如图2，当
，
，则
（直接写出结果）
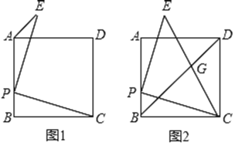
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知反比例函数
（k为常数，k≠0）的图象经过点A（2，3）．
（1）求这个函数的解析式；
（2）判断点B（-1，6），C（3，2）是否在这个函数的图象上，并说明理由；
（3）当-3＜x＜-1时，求y的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校八年级有800名学生，在一次跳绳模拟测试中，从中随机抽取部分学生，根据其测试成绩制作了下面两个统计图，请根据相关信息，解答下列问题：
（1）本次抽取到的学生人数为______，扇形统计图中
的值为______．
（2）本次调查获取的样本数据的众数是_____（分），中位数是_____（分）．
（3）根据样本数据，估计我校八年级模拟体测中得12分的学生约有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，这是人民公园的景区示意图．以中心广场为原点，分别以正东、正北 方向为 x 轴、y 轴正方向建立平面直角坐标系，规定一个单位长度代表 100m 长．已知 各建筑物都在坐标平面网格的格点上，且东门的坐标为(400，0)．
(1)请写出图中下列地点的坐标：
牡丹园 ； 游乐园 ；
(2)连接音乐台、湖心亭和望春亭这三个 地点，画出所得的三角形．然后将所 得三角形向下平移 200m，画出平移后的图形；
(3)问题(2)中湖心亭平移后的对应点的坐标为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
