
【题目】已知正方形![]() ,
,![]() 为边
为边![]() 上一点
上一点![]() 不与
不与![]() 、
、![]() 重合),过
重合),过![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() .
.
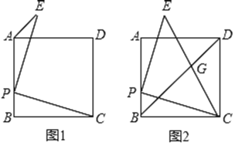
(1)如图1,求![]() 的度数;
的度数;
(2)如图2,连接![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() ;
;
(3)如图2,当![]() ,
,![]() ,则
,则![]() (直接写出结果)
(直接写出结果)
【答案】(1)∠EAD=45°;(2)证明见详解;(3)![]()
【解析】
(1)如图1中,作EH⊥BA于H.只要证明△HPE≌△CBP,推出BC=PH=AB,HE=PB,推出PB=AH=EH,推出∠HAE=45°,即可解决问题;
(2)作EK∥AB交BD于K.首先证明四边形ABKE是平行四边形,再证明△GEK≌△GCD,可得GD=GK,根据BD=![]() CD,即可解决问题;
CD,即可解决问题;
(3)利用(1)(2)中结论即可解决问题;
(1)如图1中,作EH⊥BA于H.
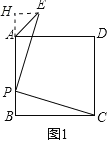
∵四边形ABCD是正方形,
∴∠B=∠BAD=∠HAD=90°,AB=BC,
∵EP⊥PC,
∴∠EPC=90°,
∴∠BPC+∠HPE=90°,∠BPC+∠BCP=90°,
∴∠HPE=∠BCP,
在△HPE和△CBP中,

∴△HPE≌△CBP,
∴BC=PH=AB,HE=PB,
∴PB=AH=EH,
∴∠HAE=45°,
∴∠EAD=45°.
(2)证明:作EK∥AB交BD于K.
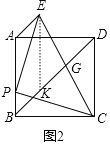
∵∠EAD=∠ADB=45°,
∴AE∥BK,
∵AB∥EK,
∴四边形ABKE是平行四边形,
∴EK=AB=CD,AE=BK,
∵AB∥CD,∴EK∥CD,
∴∠GEK=∠GCD,
∴△GEK≌△GCD,
∴GD=GK,
∵BD=![]() CD,BD=BK+DK=AE+2DG,
CD,BD=BK+DK=AE+2DG,
∴AE+2DG=![]() CD.
CD.
(3)由(1)可知AE=![]() ,由(2)可知
,由(2)可知![]() +2DG=
+2DG=![]() ,
,
∴DG=![]() ,
,
∵BD=![]() ,
,
∴BG=![]()


科目:初中数学 来源: 题型:
【题目】如图,三角形纸片ABC中,∠B=2∠C,把三角形纸片沿直线AD折叠,点B落在AC边上的E处,那么下列等式成立的是( )

A.AC=AD+BDB.AC=AB+BDC.AC=AD+CDD.AC=AB+CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课外兴趣小组在本校学生中开展“感动中国2014年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |

(1)表中的a=________,b=________;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=-x+(k+13)和反比例函数![]() 的图象相交于点A与点B.过A点作AC⊥x轴于点C,S△AOC=6.
的图象相交于点A与点B.过A点作AC⊥x轴于点C,S△AOC=6.

(1)求反比例函数和一次函数的解析式;
(2)求点A与点B的坐标;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
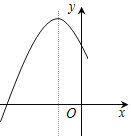
【题目】如图是二次函数![]() 图象的一部分,图象过点A(-3,0),对称轴为直线
图象的一部分,图象过点A(-3,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若B(
;④若B(![]() ,
, ![]() )、C(
)、C(![]() ,
, ![]() )为函数图象上的两点,则
)为函数图象上的两点,则![]() .其中正确结论是( )
.其中正确结论是( )
A. ②④ B. ①③ C. ①④ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化商店计划同时购进A、B两种仪器,若购进A种仪器2台和B种仪器3台,共需要资金1700元;若购进A种仪器3台,B种仪器1台,共需要资金1500元.
(1)求A、B两种型号的仪器每台进价各是多少元?
(2)已知A种仪器的售价为760元/台,B种仪器的售价为540元/台.该经销商决定在成本不超过30000元的前提下购进A、B两种仪器,若B种仪器是A种仪器的3倍还多10台,那么要使总利润不少于21600元,该经销商有哪几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形ABC的三个顶点的坐标分别是A(0,3),B(0,1),C(2,1).若将三角形ABC向左平移3个单位长度,再向下平移1个单位长度得到三角形A′B′C′.
(1)写出三角形A′B′C′各顶点的坐标;
(2)画出三角形ABC和三角形A′B′C′;
(3)求出三角形A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,六边形 ABCDEF 中,∠A+∠B+∠C=∠D+∠E+∠F,猜想可 得六边形 ABCDEF 中必有两条边是平行的.

(1)根据图形写出你的猜想: ∥ ;
(2)请证明你在(1)中写出的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com