
【题目】如图,这是人民公园的景区示意图.以中心广场为原点,分别以正东、正北 方向为 x 轴、y 轴正方向建立平面直角坐标系,规定一个单位长度代表 100m 长.已知 各建筑物都在坐标平面网格的格点上,且东门的坐标为(400,0).

(1)请写出图中下列地点的坐标:
牡丹园 ; 游乐园 ;
(2)连接音乐台、湖心亭和望春亭这三个 地点,画出所得的三角形.然后将所 得三角形向下平移 200m,画出平移后的图形;
(3)问题(2)中湖心亭平移后的对应点的坐标为 .
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=-x+(k+13)和反比例函数![]() 的图象相交于点A与点B.过A点作AC⊥x轴于点C,S△AOC=6.
的图象相交于点A与点B.过A点作AC⊥x轴于点C,S△AOC=6.

(1)求反比例函数和一次函数的解析式;
(2)求点A与点B的坐标;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC,点D和点B关于直线AC轴对称.点M(不同于点A和点C)在射线CA上,线段DM的垂直平分线交直线BC的于N,
(1)如图,过点D作DE⊥BC,交BC的延长线于E,若CE=5,求BC的长;
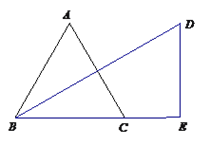
(2)如图,若点M在线段AC上,求证:△DMN为等边三角形;

(3)连接CD,BM,若![]() ,直接写出
,直接写出![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出利用尺规作图完成下面问题:

已知:∠ACB是△ABC的一个内角.
求作:∠APB=∠ACB.
小路的作法如下:

老师说:“小路的作法正确.”
请回答:(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是_____;
(2)∠APB=∠ACB的依据是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,六边形 ABCDEF 中,∠A+∠B+∠C=∠D+∠E+∠F,猜想可 得六边形 ABCDEF 中必有两条边是平行的.

(1)根据图形写出你的猜想: ∥ ;
(2)请证明你在(1)中写出的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过⊙C上一点P作⊙C的切线l.当入射光线照射在点P处时,产生反射,且满足:反射光线与切线l的夹角和入射光线与切线l的夹角相等,点P称为反射点.规定:光线不能“穿过”⊙C,即当入射光线在⊙C外时,只在圆外进行反射;当入射光线在⊙C内时,只在圆内进行反射.特别地,圆的切线不能作为入射光线和反射光线.光线在⊙C外反射的示意图如图1所示,其中∠1=∠2.

(1)自⊙C内一点出发的入射光线经⊙C第一次反射后的示意图如图2所示,P1是第1个反射点.请在图2中作出光线经⊙C第二次反射后的反射光线和反射点P3;
(2)当⊙O的半径为1时,如图3:
①第一象限内的一条入射光线平行于y轴,且自⊙O的外部照射在圆上点P处,此光线经⊙O反射后,反射光线与x轴平行,则反射光线与切线l的夹角为___________°;
②自点M(0,1)出发的入射光线,在⊙O内顺时针方向不断地反射.若第1个反射点是P1,第二个反射点是P2,以此类推,第8个反射点是P8恰好与点M重合,则第1个反射点P1的坐标为___________;
(3)如图4,点M的坐标为(0,2),⊙M的半径为1.第一象限内自点O出发的入射光线经⊙M反射后,反射光线与坐标轴无公共点,求反射点P的纵坐标的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线AB与x轴、y轴相交于![]() 、
、![]() 两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转
两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转![]() 得到CD,当点D恰好落在直线AB上时,过点D作
得到CD,当点D恰好落在直线AB上时,过点D作![]() 轴于点E.
轴于点E.

(1)求证,![]() ;
;
(2)如图2,将![]() 沿x轴正方向平移得
沿x轴正方向平移得![]() ,当直线
,当直线![]() 经过点D时,求点D的坐标及
经过点D时,求点D的坐标及![]() 平移的距离;
平移的距离;

(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=24,BC=26,CA=14.顺次连接△ABC各边中点,得到△A1B1C1;再顺次连接△A1B1C1各边中点,得到△A2B2C2…如此进行下去,得到![]() ,则△A8B8C8的周长为( )
,则△A8B8C8的周长为( )

A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com