
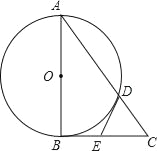
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E为BC的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)求证:4DE2=CDAC.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)如图,作辅助线;根据题意结合图形,证明∠ODE=90°,即可解决问题;
(2)根据圆周角定理得到∠ADB=∠BDC=90°,根据直角三角形的性质得到BC=2DE,根据相似三角形的性质即可得到结论.
(1)证明:连接OD、BD,
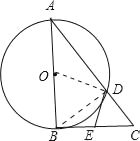
∵AB为⊙O的直径,
∴∠ADB=∠CDB=90°;
又∵点E为BC的中点,
∴BE=DE,
∴∠BDE=∠EBD;
∵OA=OD,
∴∠OAD=∠ODA;
又∵∠OAD+∠OBD=90°,∠EBD+∠OBD=90°,
∴∠OAD=∠EBD,即∠ODA=∠BDE;
∴∠ODE=∠BDE+∠ODB=∠ODA+∠ODB=90°,
又∵点D在⊙O上,
∴DE是圆⊙O的切线;
(2)∵AB为⊙O的直径,
∴∠ADB=∠BDC=90°,
∵点E为BC的中点,
∴BC=2DE,
∵∠ABC=90°,
∴∠ABC=∠BDC,
∵∠C=∠C,
∴△ABC∽△BDC,
∴![]() ,
,
∴BC2=CDAC,
∴4DE2=CDAC.


科目:初中数学 来源: 题型:
【题目】在不透明的布袋中装有1个红球,2个白球,它们除颜色外其余完全相同.
(1)从袋中任意摸出两个球,试用树状图或表格列出所有等可能的结果,并求摸出的球恰好是两个白球的概率;
(2)若在布袋中再添加a个白球,充分搅匀,从中摸出一个球,使摸到红球的概率为![]() ,试求a的值.
,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个木制的棱长为3的正方体的表面涂上颜色,将它的棱三等分,然后从等分点把正方体锯开,得到27个棱长为l的小正方体,将这些小正方体充分混合后,装入口袋,从这个口袋中任意取出一个小正方体,则这个小正方体的表面恰好涂有两面颜色的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
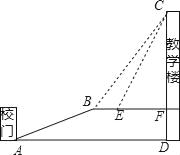
【题目】重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i.
(2)求DC的长.
(参考数据:tan53°≈![]() ,tan63.4°≈2)
,tan63.4°≈2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l1∥l2∥l3,且l1与l2的距离为1.l2与l3的距离为2,把∠ACB=30°的直角三角板如图放置,顶点A,B,C恰好落在三条直线上,则线段AB的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD 中,AE=AB,直线 DE 交 BC 于点 F,则∠BED 的度数是( )
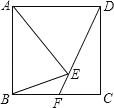
A. 105° B. 120° C. 135° D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数,若售价30元,能卖200台/月,若售价35元,能卖150台/月.
(1)求y与x的函数关系式.
(2)为清理库存,在不赔钱的情况下,售价定为多少元时,每月可获得最大销售量?
(3)如果想要每月获得2000元的利润,那么销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com