
如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).

(1)两建筑物底部之间水平距离BD的长度为60米;
(2)建筑物CD的高度为(60﹣20 )米.
)米.
【解析】
试题分析:(1)由题意得:BD∥AE,从而得到∠BAD=∠ADB=45°,再由BD=AB=60,求得两建筑物底部之间水平距离BD的长度为60米;
(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,根据AF=BD=DF=60,在Rt△AFC中利用∠FAC=30°求得CF,然后即可求得CD的长.
试题解析:(1)根据题意得:BD∥AE,
∴∠ADB=∠EAD=45°,
∵∠ABD=90°,
∴∠BAD=∠ADB=45°,
∴BD=AB=60,
∴两建筑物底部之间水平距离BD的长度为60米;
(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,
∴AF=BD=DF=60,
在Rt△AFC中,∠FAC=30°,
∴CF=AF•tan∠FAC=60× =20
=20 ,
,
又∵FD=60,
∴CD=60﹣20 ,
,
∴建筑物CD的高度为(60﹣20 )米.
)米.

考点:解直角三角形的应用


科目:初中数学 来源:2014年初中毕业升学考试(黑龙江绥化卷)数学(解析版) 题型:填空题
如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2014个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江大庆卷)数学(解析版) 题型:解答题
关于x的函数y=(m2-1)x2-(2m+2)x+2的图象与x轴只有一个公共点,求m的值.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江大庆卷)数学(解析版) 题型:选择题
已知反比例函数的图象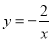 上有两点A(x1,y1)、B(x2,y2),若y1>y2,则x1-x2的值是( )
上有两点A(x1,y1)、B(x2,y2),若y1>y2,则x1-x2的值是( )
A.正数 B.负数 C.非正数 D.不能确定
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江大庆卷)数学(解析版) 题型:选择题
下列式子中成立的是( )
A.-|-5|>4 B.-3<|-3| C.-|-4|=4 D.|- 5.5|<5
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江哈尔滨卷)数学(解析版) 题型:填空题
如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(青海西宁卷)数学(解析版) 题型:解答题
如图,已知?ABCD水平放置在平面直角坐标系xOy中,若点A,D的坐标分别为(-2,5),(0,1),点B(3,5)在反比例函数y= (x>0)图象上.
(x>0)图象上.
(1)求反比例函数y= 的解析式;
的解析式;
(2)将?ABCD沿x轴正方向平移10个单位后,能否使点C落在反比例函数y= 的图象上?并说明理由.
的图象上?并说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(重庆A卷)数学(解析版) 题型:选择题
如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,过点F作FG⊥FE,交直线AB于点G.若∠1=42°,则∠2的大小是( )

A.56° B.48° C.46° D.40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com