练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．如图，要在燃气管道l上修建一个泵站，分别向A，B两镇供气，泵站修在管道的什么地方，可使所用的输气管线最短？你可以在l上找几个点试一试，能发现什么规律？

    分析 根据在直线l上的同侧有两个点A、B，在直线L上有到A、B的距离之和最短的点存在，可以通过轴对称来确定，即作出其中一点关于直线l的对称点，对称点与另一点的连线与直线l的交点就是所要找的点．

    解答 解：如图所示，
    作A点关于直线的对称点A′，连接A′B，直线与河的交点即是所求的点．
    此时军官从军营A出发先到P点，再去同侧的B地开会路途最短．

    点评 此题主要考查了最短路线问题，涉及最短距离的问题，一般要考虑线段的性质定理，结合本节所学轴对称变换来解决，多数情况要作点关于某直线的对称点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    16．如图，直角三角形纸片ABC中AB=3，AC=4，D为斜边BC中点，第1次将纸片折叠，使点A与点D重合，折痕与AD交于点P1；设P1D的中点为D1，第2次将纸片折叠，使点A与点D1重合，折痕与AD交于P2；设P2D1的中点为D2，第3次将纸片折叠，使点A与点D2重合，折痕与AD交于点P3；设Pn-1Dn-2的中点为Dn-1，第n次将纸片折叠，使点A与点Dn-1重合，折痕与AD交于点Pn（n＞2），则AP6的长为（　　）
    A．$\frac{{3}^{5}}{5×{2}^{9}}$B．$\frac{5×{3}^{5}}{{2}^{12}}$C．$\frac{5×{3}^{6}}{{2}^{14}}$D．$\frac{{3}^{7}}{5×{2}^{11}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

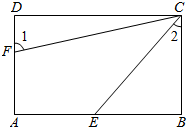    3．如图，已知四边形ABCD是平行四边形，并且∠A=∠D．
    （1）求证：四边形ABCD为矩形；
    （2）点E是AB边的中点，F为AD边上一点，∠1=2∠2，若CE=4，CF=5，求DF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．一小商店一周的盈亏情况如表（亏为负），单位：元
    星期周一周二周三周四周五周六周日
    盈亏情况128.3-25.6-1527-736.598
    （1）计算出小商店一周的盈亏情况；
    （2）指出盈利最多一天的盈利额．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知函数f（x）=x2+bx+c，方程f（x）=x的两个根x1，x2，且x1-x2＞2．
    （1）求证；x1，x2也是方程f（f（x））=x的根；
    （2）设f（f（x））=x的另两个根是x3，x4，且x3＞x4．试判断x1，x2，x3，x4的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．某品牌饮水机厂生产一种饮水机和饮水机槽，饮水机每台定价350元，饮水机桶每只定价50元，厂方在开展促销活动期间，可以同时向客户提供两种优惠方案：
    ①买一台饮水机送一只饮水机桶；
    ②饮水机和饮水机桶都按定价的90%付款，现某客户要到该饮水机厂购买饮水机30台，饮水机桶x只（x超过30）．
    （1）若该客户按方案①购买，求客户需付款（用含x的式子表示）；
    若该客户按方案②购买，求客户需付款（用含x的式子表示）；
    （2）若x=40，通过计算说明此时按哪种方案购买较为合算？
    （3）当x=40时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法，并计算出所需的钱数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

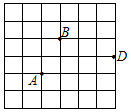    4．如图，在6×6的正方形网格中，每个小正方形边长都是1，每个小正方形的顶点叫做格点．A、B两格点位置如图所示．
    （1）在如图正方形网格中找格点C，使△ABC是等腰直角三角形，问：满足条件的点C有4个；
    （2）如图，点D为正方形网格的格点，试求△ABD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．以x为自变量的二次函数y=-x2+（2m+2）x-（m2+4m-3）中，m为不小于0的整数，它的图象与x轴的交点A在原点左边，交点B在原点右边．
    （1）求这个二次函数的解析式；
    （2）设点C为此二次函数图象上的一点，且满足△ABC的面积等于10，请求出点C的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：$\frac{3}{5}$-3.7-（-$\frac{2}{5}$）-1.3．

    查看答案和解析>>

    同步练习册答案