
【题目】如图,在每个小正方形的边长为![]() 的网格中,点A,B,C在格点上,以点A为圆心、AC为半径的半圆交AB于点 E.
的网格中,点A,B,C在格点上,以点A为圆心、AC为半径的半圆交AB于点 E.
(1)BE的长为________;
(2)请用无刻度的直尺,在如图所示的网格中,找一点P(点P,C 在AB两侧),使PA=5,PE与半圆相切. 简要说明点P的位置是如何找到的.
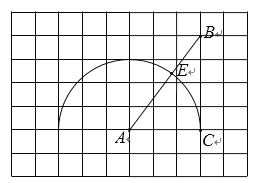
【答案】(1)2;(2)图见解析,理由见解析.
【解析】
(1)先结合网格的特点可得![]() ,再根据勾股定理可得
,再根据勾股定理可得![]() ,然后根据圆的性质可得
,然后根据圆的性质可得![]() ,最后根据线段的和差即可得;
,最后根据线段的和差即可得;
(2)取格点![]() ,分别作直线
,分别作直线![]() ,两直线相交于点P,点P即为所作;理由:先根据平行四边形的判定与性质得出
,两直线相交于点P,点P即为所作;理由:先根据平行四边形的判定与性质得出![]() ,再根据三角形全等的判定定理与性质得出
,再根据三角形全等的判定定理与性质得出![]() ,然后根据三角形中位线定理、垂直平分线的判定与性质可得
,然后根据三角形中位线定理、垂直平分线的判定与性质可得![]() ,由此即可得证.
,由此即可得证.
(1)由网格的特点得:![]()
![]()
由圆的性质得:![]()
![]()
故答案为:2;
(2)如图,取格点![]() ,分别作直线
,分别作直线![]() ,两直线相交于点P,则点P即为所作,理由如下:
,两直线相交于点P,则点P即为所作,理由如下:
由网格的特点得:![]() ,
,![]() ,
,![]()
![]() 四边形ABGF是平行四边形
四边形ABGF是平行四边形
![]()
在![]() 和
和![]() 中,
中,
![]()
![]() ,即
,即![]()
![]() 与半圆相切
与半圆相切
![]() ,即点A是DF的中点,且
,即点A是DF的中点,且![]()
![]() 是
是![]() 的中位线,点E是DP的中点
的中位线,点E是DP的中点
![]() 垂直平分DP
垂直平分DP
![]()
综上,点P即为所作.



科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
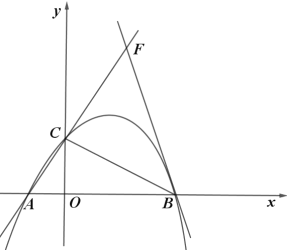
(1)求抛物线的函数表达式;
(2)点![]() 为
为![]() 轴右侧抛物线上一点,是否存在点
轴右侧抛物线上一点,是否存在点![]() 使
使![]() ?若存在,求出点
?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(3)将直线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,求直线
,求直线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在百货商场购进了A、B两种品牌的篮球,购买A品牌蓝球花费了2400元,购买B品牌蓝球花费了1950元,且购买A品牌蓝球数量是购买B品牌蓝球数量的2倍,已知购买一个B品牌蓝球比购买一个A品牌蓝球多花50元.
(1)求购买一个A品牌、一个B品牌的蓝球各需多少元?
(2)该学校决定再次购进A、B两种品牌蓝球共30个,恰逢百货商场对两种品牌蓝球的售价进行调整,A品牌蓝球售价比第一次购买时提高了10%,B品牌蓝球按第一次购买时售价的9折出售,如果这所中学此次购买A、B两种品牌蓝球的总费用不超过3200元,那么该学校此次最多可购买多少个B品牌蓝球?
查看答案和解析>>
科目:初中数学 来源: 题型:
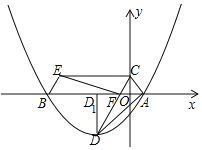
【题目】如图,在平面直角坐标系中,抛物线与x轴交于点A(1, 0),B(-7, 0),顶点D坐标为(-3,![]() ),点C在y轴的正半轴上,CD交x轴于点F,△CAD绕点C顺时针旋转得到△CFE,点A恰好旋转到点F,连接BE.过顶点D作DD1⊥x轴于点D1
),点C在y轴的正半轴上,CD交x轴于点F,△CAD绕点C顺时针旋转得到△CFE,点A恰好旋转到点F,连接BE.过顶点D作DD1⊥x轴于点D1
(1)求抛物线的表达式
(2)求证:四边形BFCE是平行四边形.
(3)点P是抛物线上一动点,当P在B点左侧时,过点P作PM⊥x轴,点M为垂足,请问是否存在P点使得△PAM与△DD1A相似,如果存在,请写出点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划经销一些特产,经销前,围绕“A:王高虎头鸡,B:羊口咸蟹子,C:桂河芹菜,D:巨淀湖咸鸭蛋”四种特产,在全市范围内随机抽取了部分市民进行问卷调查:“我最喜欢的特产是什么?”(必选且只选一种).现将调查结果整理后,绘制成如图所示的不完整的扇形统计图和条形统计图.

(1)请补全扇形统计图和条形统计图;
(2)若全市有110万市民,估计全市最喜欢“羊口咸蟹子”的市民约有多少万人?
(3)在一个不透明的口袋中有四个分别写上四种特产标记A、B、C、D的小球(除标记外完全相同),随机摸出一个小球然后放回,混合摇匀后,再随机摸出一个小球,则两次都摸到A的概率是多少?写出分析计算过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个种子店都销售“黄金1号”玉米种子.在甲店,该种子的价格为 5元 / kg,如果一次购买2 kg 以上的种子,超过 2 kg 部分的种子的价格打8折.在乙店,不论一次购买该种子的数量是多少,价格均为4.5 元 / kg.
(1)根据题意,填写下表:

(2)设一次购买种子的数量为![]() kg(
kg(![]() ). 在甲店购买的付款金额记为
). 在甲店购买的付款金额记为![]() 元,在乙店购买的付款金额为
元,在乙店购买的付款金额为![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3) 若在同一店中一次购买种子的付款金额是36元,则最多可购买种子______ kg.若在同一店中一次购买种子10 kg,则最少付款金额是________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,半径OA丄OB,点D在OA或OA的延长线上(不与点O,A重合),直线BD交⊙O于点C,过C作⊙O的切线交直线OA于点P.
(1)如图(1),点D在线段OA上,若∠OBC=15°, 求∠OPC的大小;
(2)如图(2),点D在OA的延长线上,若∠OBC=65°,求∠OPC的大小.
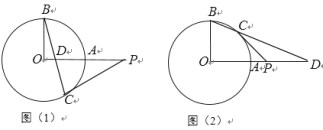
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某翻译团为成为2022年冬奥会志愿者做准备,该翻译团一共有五名翻译,其中一名只会翻译西班牙语,三名只会翻译英语,还有一名两种语言都会翻译.
(1)求从这五名翻译中随机挑选一名会翻译英语的概率;
(2)若从这五名翻译中随机挑选两名组成一组,请用树状图或列表的方法求该纽能够翻译上述两种语言的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两条邻边长分别为![]() ,1的矩形纸片剪成四个等腰三角形纸片(无余纸片),各种剪法剪出的等腰三角形中,其中一个等腰三角形的腰长可以是下列数中的_____(填序号).
,1的矩形纸片剪成四个等腰三角形纸片(无余纸片),各种剪法剪出的等腰三角形中,其中一个等腰三角形的腰长可以是下列数中的_____(填序号).
①![]() ,②1,③
,②1,③![]() ﹣1,④
﹣1,④![]() ,⑤
,⑤![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com