解:(1)过A作AM⊥BC于M,则四边形AMCD是矩形;
∴AD=MC=9cm,AM=CD=12cm;
Rt△ABM中,AM=12cm,BM=BC-MC=6cm;
由勾股定理,得:AB=6

cm(只写答案给1分)
(2)当PE∥CD时△AEP∽△ADC
∴

=
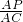
∵∠D=90°,AD=9cm,CD=12cm,
∴AC=

.=

=15cm
∴AP=15-t
∴
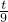
=
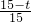
解得t=
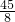
(符合题意)
∴当PE∥CD时,t=
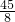
;
(3)①过点E,F作EG⊥AC于G,FH⊥AC于H.
易证AQ=AE=t
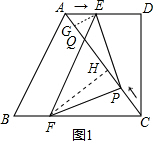
在Rt△ADC中,sin∠DAC=
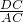
=
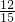
=

∴EG=AE×sin∠DAC=

t;
∵AD∥BC
∴∠ACB=∠DAC
∴FH=CF×sin∠CAB=

(15-t)=12-

t
∴S
△PEF=S
△PQE+S
△PQF=
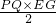
+
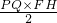
=
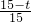

(

t+12-

t)=-12t+90;
②易知:AE=CP=t,AP=CF=CQ=15-t,∠EAP=∠FCP,
∴△AEP≌△CPF,∴EP=PF;
∵EF是⊙O的直径
∴∠EPF=90°;
∴△EPF是等腰直角三角形;
易知EF=AB=6

cm;
∴S=

×6

×3

=45cm
2;
代入①的函数关系式,得:
-12t+90=45,解得t=

.
分析:(1)过A作BC的垂线,设垂足为M,在Rt△ABM中,由勾股定理即可求得AB的长;
(2)当PE∥CD时,△AEP∽△ADC,可用t表示出CP、AP、AE的长,进而由相似三角形得到的比例线段求得t的值;
(3)①易知BC=AC=15,则△ABC是等腰三角形,由于AE∥BC,易证得△AEQ、△CFQ也是等腰三角形,则AE=AQ=t,CQ=CF=15-t;可分别过E、F作AC的垂线,设垂足为G、H,根据∠DAC、∠BCA的正弦值即可得到EG、FH的表达式,进而可求得△PQE、△PQF的面积表达式,两者的面积和即为△PEF的面积,由此可得到S、t的函数关系式;
②由①知:AE=CP=t,CF=CQ=15-t,且∠DAC=∠BCA,即可证得△AEP≌△CPF,得PE=PF;若△PEF的外接圆圆心是EF的中点,那么此时△PEF是等腰Rt△,已求得EF(即AB)的长,进而可得到△PEF的面积,然后将S的值代入①的函数关系式中即可求得t的值.
点评:此题考查了直角梯形的性质、勾股定理、圆周角定理、等腰三角形和相似三角形的判定和性质等知识的综合应用能力.



 cm(只写答案给1分)
cm(只写答案给1分) =
=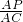
 .=
.= =15cm
=15cm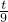 =
=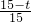
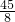 (符合题意)
(符合题意)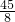 ;
;
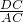 =
=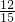 =
=
 t;
t; (15-t)=12-
(15-t)=12- t
t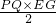 +
+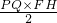 =
=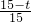
 (
( t+12-
t+12- t)=-12t+90;
t)=-12t+90; cm;
cm; ×6
×6 ×3
×3 =45cm2;
=45cm2; .
.

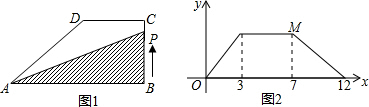
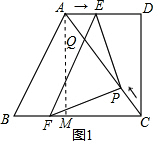
 如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )