练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．计算与化简求值
    （1）12-（-18）+（-7）-15
    （2）-23+（-15）÷（-3）-|3-4|
    （3）化简2（3x2-2xy）-4（2x2-xy-1）
    （4）先化简再求值9a2-[7a2-（2a-a2）-3a]，其中a=-3．

    分析 （1）根据有理数的减法，可统一成有理数的加法，根据有理数的加法，可得答案；
    （2）根据先算成方，再算乘除，最后算加减，可得答案；
    （3）根据去括号、合并同类项，可得答案；
    （4）根据去括号、合并同类项，可化简整式，根据代数式求值，可得答案．

    解答 解：（1）12-（-18）+（-7）-15=12+18+（-7）+（-15）=30+（-22）=8；
    （2）-23+（-15）÷（-3）-|3-4|=-8+（-15）÷（-3）-1=-8+5-1=-4；
    （3）2（3x2-2xy）-4（2x2-xy-1）=6x2-4xy-8x2+4xy+4=-2x2+4；
    （4）9a2-[7a2-（2a-a2）-3a]=9a2-[7a2-2a+a2-3a]=9a2-8a2+5a=a2+5a，
    当a=-3时，原式=（-3）2+5×（-3）=9+（-15）=-6．

    点评 本题考查了整式的化简求值，去括号是解题关键，括号前是正数去括号不变号，括号前是负数去括号全变号．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

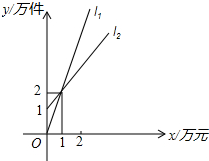    17．如图，l1表示某公司一种产品一天的销售收入与销售量的关系，l2表示该产品一天的销售成本与销售量的关系．
    （1）求x=2时，该产品的利润（销售收入减去销售成本）是多少？
    （2）每天销售多少件，销售收入等于销售成本？
    （3）求出利润与销售量的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．正比例函数y=2x与反比例函数y=$\frac{k}{x}$（k≠0）的图象有一个交点为（2，4），则另一个交点坐标为（　　）
    A．（2，-4）B．（-2，-4）C．（-2，4）D．（-2，-2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列各数中，$-\frac{22}{7}$，3.14159265，$\sqrt{9}$，$\root{3}{3}$，$\frac{π}{2}$，0，$-\sqrt{5}+2$是无理数的有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

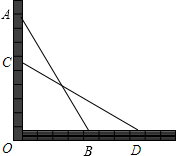    2．如图，一架长为2.5的梯子AB，斜靠在竖直的墙AO上，这时梯子底B距墙底端0的距离为0.7m，如果梯子的顶端A沿墙下滑0.4m到c处，则梯子的底端滑出的距离BD=0.8m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列说法中不正确的有（　　）
    ①-3.14既是负数，分数，也是有理数；
    ②0既不是正数，也不是负数，但是整数；
    ③0是正数和负数的分界；
    ④-200既是负数，也是整数，但不是有理数．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．若$y=（m-1）{x^{{m^2}-2}}$是反比例函数，则m=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．无论a取什么实数，点P（a-1，2a-3）都在直线l上．若点Q（m，n）也是直线l上的点，则2m-n+3的值等于（　　）
    A．4B．-4C．6D．-6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．阅读下面材料：
    如图1，在平面直角坐标系xOy中，直线y1=ax+b与双曲线y2=$\frac{k}{x}$交于A（1，3）和B（-3，-1）两点．
    观察图象可知：
    ①当x=-3或1时，y1=y2；
    ②当-3＜x＜0或x＞1时，y1＞y2，即通过观察函数的图象，可以得到不等式ax+b＞$\frac{k}{x}$的解集．
    有这样一个问题：求不等式x3+4x2-x-4＞0的解集．
    某同学根据学习以上知识的经验，对求不等式x3+4x2-x-4＞0的解集进行了探究．
    下面是他的探究过程，请将（2）、（3）、（4）补充完整：
    （1）将不等式按条件进行转化：
    当x=0时，原不等式不成立；
    当x＞0时，原不等式可以转化为x2+4x-1＞$\frac{4}{x}$；
    当x＜0时，原不等式可以转化为x2+4x-1＜$\frac{4}{x}$；
    （2）构造函数，画出图象
    设y3=x2+4x-1，y4=$\frac{4}{x}$，在同一坐标系中分别画出这两个函数的图象．
    双曲线y4=$\frac{4}{x}$如图2所示，请在此坐标系中画出抛物线y3=x2+4x-1；（不用列表）
    （3）确定两个函数图象公共点的横坐标
    观察所画两个函数的图象，猜想并通过代入函数解析式验证可知：满足y3=y4的所有x的值为±1和-4；
    （4）借助图象，写出解集
    结合（1）的讨论结果，观察两个函数的图象可知：不等式x3+4x2-x-4＞0的解集为x＞1或-4＜x＜-1．

    查看答案和解析>>

    同步练习册答案