【题目】如图，直线
表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（ ）
A.一处B.二处C.三处D.四处
【答案】D
【解析】
由三角形内角平分线的交点到三角形三边的距离相等，可得三角形内角平分线的交点满足条件；然后利用角平分线的性质，可证得三角形两条外角平分线的交点到其三边的距离也相等，这样的点有3个，可得可供选择的地址有4个．
解：∵△ABC内角平分线的交点到三角形三边的距离相等，
∴△ABC内角平分线的交点满足条件；
如图：点P是△ABC两条外角平分线的交点，
过点P作PE⊥AB，PD⊥BC，PF⊥AC，
∴PE=PF，PF=PD，
∴PE=PF=PD，
∴点P到△ABC的三边的距离相等，
∴△ABC两条外角平分线的交点到其三边的距离也相等，满足这条件的点有3个；
综上，到三条公路的距离相等的点有4处，
∴可供选择的地址有4处．
故选：D
科目：初中数学 来源： 题型：
【题目】如图，A，B两地被池塘隔开，小明通过下列方法测出了A，B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12 m，由此他就知道了A，B间的距离，有关他这次探究活动的描述错误的是( )
A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
【答案】D
【解析】试题分析：根据三角形的中位线平行于第三边并且等于第三边的一半可得MN∥AB，MN=
AB，再根据相似三角形的判定解答．
试题解析：∵M、N分别是AC，BC的中点
∴MN∥AB，MN=
AB，
∴AB=2MN=2×12=24m
△CMN∽△CAB
∵M是AC的中点
∴CM=MA
∴CM：MA=1：1
故描述错误的是D选项．
故选D．
考点：1．三角形中位线定理；2．相似三角形的应用．
【题型】单选题
【结束】
10
【题目】若关于
的一元二次方程
+x-3m=0有两个不相等的实数根,则
的取值范围是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我市自开展“学习新思想，做好接班人”主题阅读活动以来，受到各校的广泛关注和同学们的积极响应，某校为了解全校学生主题阅读的情况，随机抽查了部分学生在某一周主题阅读文章的篇数，并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7及以上 |
人数(人) | 20 | 28 | m | 16 | 12 |
请根据统计图表中的信息，解答下列问题:
(1)求被抽查的学生人数和
的值；
(2)求本次抽查的学生文章阅读篇数的中位数和众数；
(3)若该校共有800名学生，根据抽查结果估计该校学生在这一周内文章阅读的篇数为4篇的人数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知任意三角形ABC，
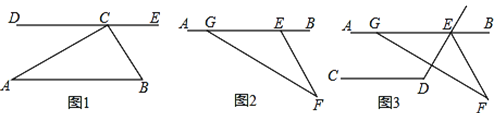
（1）如图1，过点C作DE∥AB，求证：∠DCA=∠A；
（2）如图1，求证：三角形ABC的三个内角（即∠A、∠B、∠ACB）之和等于180°；
（3）如图2，求证：∠AGF=∠AEF+∠F；
（4）如图3，AB∥CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=150°，求∠F．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=ax2+bx+1（a≠0）的图象的顶点在第一象限，且过点（-1，0）．设t=a+b+1，则t值的变化范围是（ ）
A. 0＜t＜1 B. 0＜t＜2 C. 1＜t＜2 D. -1＜t＜1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知 a，b，c 分别是△ABC 的三边长．
（1）分解因式：①ac﹣bc= ，②﹣a2+2ab﹣b2= ；
（2）若 ac﹣bc＝﹣a2+2ab﹣b2，试判断△ABC 的形状；并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图 1，O 是等边三角形 ABC 内一点，连接 OA，OB，OC，且 OA＝3，OB＝4，OC＝5，将△BAO 绕点 B 顺时针旋转后得到△BCD，连接 OD．
填空：①旋转角为 °；②线段 OD 的长是 ；③∠BDC= °；
（2）如图 2，O 是△ABC 内一点，且∠ABC＝90°，BA=BC． 连接 OA，OB，OC，将△BAO 绕点 B 顺时针旋转后得到△BCD，连接 OD．当 OA，OB，OC 满足什么条件时，∠BDC＝135°？请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
