
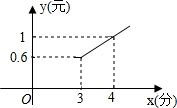
 某公用电话亭打电话时,需付电话费y(元)与通话时间x(分钟)之间的函数图象如图所示,则小明打了8分钟电话需付话费2.6元.
某公用电话亭打电话时,需付电话费y(元)与通话时间x(分钟)之间的函数图象如图所示,则小明打了8分钟电话需付话费2.6元. 分析 根据图形可得:需付电话费y(元)与通话时间 x(分钟)之间的函数关系为分段函数,分为两段:当0<x≤3时,应付的电话费为0.6元;当x>3时,设y与x的解析式为y=kx+b(k≠0),将(3,0.6)与(4,1)代入,得到关于k与b的方程组,求出方程组的解得到k与b的值,确定出此时y与x的函数解析式,然后根据打了8分钟,判断应代入x>3时的解析式,即可求出需付的费用.
解答 解:由图形可得:当0<x≤3时,y=0.6元;
当x>3时,设y与x的解析式为y=kx+b(k≠0),
将(3,0.6)与(4,1)代入得:
$\left\{\begin{array}{l}{3k+b=0.6\\;}\\{4k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=0.4}\\{b=-0.6}\end{array}\right.$,
∴y=0.4x-0.6,
∵8>3,
∴打了8分钟应付费为0.4×8-0.6=2.6元.
故答案为:2.6.
点评 此题考查了一次函数的应用,涉及的知识有:待定系数法确定函数解析式,分段函数,以及代数式求值,利用了数形结合的思想,是一道综合题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
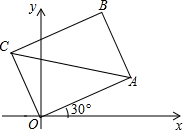 如图,矩形OABC的一顶点O恰好落在平面直角坐标系的坐标原点处,边OA与x轴正方向的夹角为30°.连结AC.若AB=6,AC=10,则点A的坐标为( )
如图,矩形OABC的一顶点O恰好落在平面直角坐标系的坐标原点处,边OA与x轴正方向的夹角为30°.连结AC.若AB=6,AC=10,则点A的坐标为( )| A. | ($4\sqrt{3}$,4) | B. | (4,4) | C. | (4,$4\sqrt{3}$) | D. | (4,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结并反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事,x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程和时间的关系,y2表示兔子所行的路程和时间的关系,回答下列问题:
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结并反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事,x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程和时间的关系,y2表示兔子所行的路程和时间的关系,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
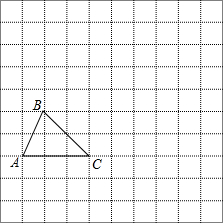 如图,在边长为1的小正方形组成的网络中,△ABC的顶点均在格点上,请按要求完成下列各题:
如图,在边长为1的小正方形组成的网络中,△ABC的顶点均在格点上,请按要求完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
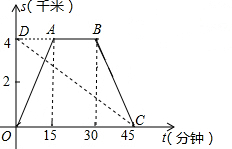 玉环中学学生小林从学校出发到玉环图书馆查阅资料,同时他的同学小丽刚好从玉环图书馆查完资料沿同一条路回学校.学校与玉环图书馆的路程是4千米,小林骑自行车,小丽步行,当小林沿原路回到学校时,小丽也刚好回到学校,图中折线O-A-B-C和线段DC分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
玉环中学学生小林从学校出发到玉环图书馆查阅资料,同时他的同学小丽刚好从玉环图书馆查完资料沿同一条路回学校.学校与玉环图书馆的路程是4千米,小林骑自行车,小丽步行,当小林沿原路回到学校时,小丽也刚好回到学校,图中折线O-A-B-C和线段DC分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC=4$\sqrt{5}$,sinC=$\frac{2\sqrt{5}}{5}$
如图,在△ABC中,AB=AC=4$\sqrt{5}$,sinC=$\frac{2\sqrt{5}}{5}$查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com