
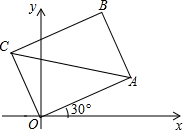
 如图,矩形OABC的一顶点O恰好落在平面直角坐标系的坐标原点处,边OA与x轴正方向的夹角为30°.连结AC.若AB=6,AC=10,则点A的坐标为( )
如图,矩形OABC的一顶点O恰好落在平面直角坐标系的坐标原点处,边OA与x轴正方向的夹角为30°.连结AC.若AB=6,AC=10,则点A的坐标为( )| A. | ($4\sqrt{3}$,4) | B. | (4,4) | C. | (4,$4\sqrt{3}$) | D. | (4,2) |
分析 在直角△ABC中利用勾股定理求得BC的长,则OA即可求得,然后在直角△OAD中利用勾股定理即可求得AD和OD的长,则A的坐标即可求得.
解答 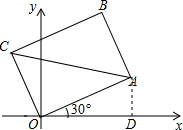 解:在直角△ABC中,BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
解:在直角△ABC中,BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
则OA=BC=8.
在直角△OAD中,AD=OA•sin∠AOD=8×$\frac{1}{2}$=4,
OD=OA•cos∠AOD=8×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$.
则A的坐标是(4$\sqrt{3}$,4).
故选A.
点评 本题考查了平行四边形的性质以及勾股定理和三角函数,正确求得OA的长是关键.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(3,1),B(-1,n),不等式ax+b≥$\frac{k}{x}$的解集是-1≤x<0或x≥3.
如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(3,1),B(-1,n),不等式ax+b≥$\frac{k}{x}$的解集是-1≤x<0或x≥3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
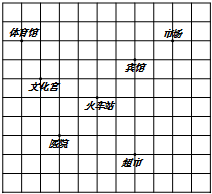 (1)如图,若以火车站为坐标原点,建立平面直角坐标系,超市的坐标为:(2,-3),则市场的坐标:(4,3),文化宫的坐标:(-3,1);
(1)如图,若以火车站为坐标原点,建立平面直角坐标系,超市的坐标为:(2,-3),则市场的坐标:(4,3),文化宫的坐标:(-3,1);查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (4,2) | B. | (-2,4) | C. | (-4,2) | D. | (2,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
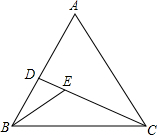 如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E.连接BE,∠BED=60°.若CE=6,△ACD的面积为$12\sqrt{3}$,则线段DB的长为4.
如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E.连接BE,∠BED=60°.若CE=6,△ACD的面积为$12\sqrt{3}$,则线段DB的长为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com