
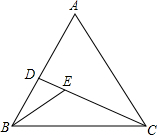
 如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E.连接BE,∠BED=60°.若CE=6,△ACD的面积为$12\sqrt{3}$,则线段DB的长为4.
如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E.连接BE,∠BED=60°.若CE=6,△ACD的面积为$12\sqrt{3}$,则线段DB的长为4. 分析 延长BE交AC边于点F,易证△ACD≌△CBF,得BF=CD,利用三角形的面积求出BF的长度,继而求出DE的长度;然后证明△BED∽△CBD,求得BD的长度4.
解答 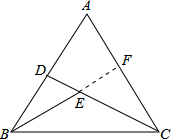 解:如图,延长BE交AC边于点F,
解:如图,延长BE交AC边于点F,
因为∠FCD+∠DCB=60°,∠DEB=∠EBC+∠ECB=60°,
∴∠ACD=∠FBC,
在△ACD和△CBF中,
$\left\{\begin{array}{l}{∠ACB=∠BAC}\\{∠FBC=∠ACD}\\{AC=BD}\end{array}\right.$
∴△ACD≌△CBF,
∴BF=CD,
S△ACD=12$\sqrt{3}$=S△CBF=$\frac{1}{2}$CE•EF•sin60°+$\frac{1}{2}$CE•BE•sin60°
=$\frac{1}{2}$CE•BF•sin60°,
∴BF=8,则DE=2,∠DBE=∠DCB,∠DEB=∠DBC=90°,
△BED∽△CBD,
∴BD2=DE•CD=16,
∴BD=4.
故答案为:4.
点评 本题考查了三角形全等的判定,以及三角形的相似的判定,运用三角形相似对应线段成比例求线段长度是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | C. | 2$\sqrt{\frac{1}{2}}$=$\sqrt{2}$ | D. | 3÷$\sqrt{2}$=2$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
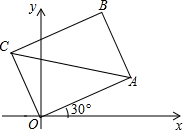 如图,矩形OABC的一顶点O恰好落在平面直角坐标系的坐标原点处,边OA与x轴正方向的夹角为30°.连结AC.若AB=6,AC=10,则点A的坐标为( )
如图,矩形OABC的一顶点O恰好落在平面直角坐标系的坐标原点处,边OA与x轴正方向的夹角为30°.连结AC.若AB=6,AC=10,则点A的坐标为( )| A. | ($4\sqrt{3}$,4) | B. | (4,4) | C. | (4,$4\sqrt{3}$) | D. | (4,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结并反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事,x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程和时间的关系,y2表示兔子所行的路程和时间的关系,回答下列问题:
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结并反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事,x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程和时间的关系,y2表示兔子所行的路程和时间的关系,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
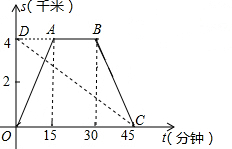 玉环中学学生小林从学校出发到玉环图书馆查阅资料,同时他的同学小丽刚好从玉环图书馆查完资料沿同一条路回学校.学校与玉环图书馆的路程是4千米,小林骑自行车,小丽步行,当小林沿原路回到学校时,小丽也刚好回到学校,图中折线O-A-B-C和线段DC分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
玉环中学学生小林从学校出发到玉环图书馆查阅资料,同时他的同学小丽刚好从玉环图书馆查完资料沿同一条路回学校.学校与玉环图书馆的路程是4千米,小林骑自行车,小丽步行,当小林沿原路回到学校时,小丽也刚好回到学校,图中折线O-A-B-C和线段DC分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com