
【题目】如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.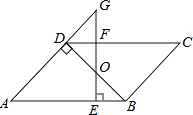
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
【答案】
(1)
证明:∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠OBE=∠ODF.
在△OBE与△ODF中,
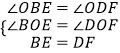
∴△OBE≌△ODF(AAS).
∴BO=DO.
(2)
解:∵EF⊥AB,AB∥DC,
∴∠GEA=∠GFD=90°.
∵∠A=45°,
∴∠G=∠A=45°.
∴AE=GE
∵BD⊥AD,
∴∠ADB=∠GDO=90°.
∴∠GOD=∠G=45°.
∴DG=DO,
∴OF=FG=1,
由(1)可知,OE=OF=1,
∴GE=OE+OF+FG=3,
∴AE=3.
【解析】1)由平行四边形的性质和AAS证明△OBE≌△ODF,得出对应边相等即可;(2)证出AE=GE,再证明DG=DO,得出OF=FG=1,即可得出结果.
【考点精析】掌握平行四边形的性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】 已知△ABC中,∠A=25°,∠B=40°. 
(1)求作:⊙O,使得⊙O经过A、C两点,且圆心O落在AB边上.(要求尺规作图,保留作图痕迹,不必写作法)
(2)求证:BC是(1)中所作⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF. 
(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)求证:OD=OE;
(3)求证:PF是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,且AC平分∠BAD,点E为AB的延长线上一点,且∠ECB=∠CAD.
(1)填空:∠ACB= ,理由是
(2)求证:CE与⊙O相切
(3)若AB=6,CE=4,求AD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.
(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中,是木杆和旗杆竖在操场上,其中木杆在阳光下的影子已画出.
(1)用线段表示这一时刻旗杆在阳光下的影子.
(2)比较旗杆与木杆影子的长短.
(3)图中是否出现了相似三角形?
(4)为了出现这样的相似三角形,木杆不可以放在图中的哪些位置?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F . 过点E作EG∥BC , 交AB于G , 则图中相似三角形有( ) 
A.4对
B.5对
C.6对
D.7对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com