
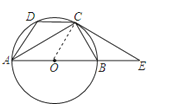
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,且AC平分∠BAD,点E为AB的延长线上一点,且∠ECB=∠CAD.
(1)填空:∠ACB= ,理由是
(2)求证:CE与⊙O相切
(3)若AB=6,CE=4,求AD的长
【答案】
(1)90°;直径所对的圆周角是直角
(2)
解:连接OC,则∠CAO=∠ACO,
∵AC平分∠BAB,
∴∠BAC=∠CAD,
∵∠ECB=∠CAD.
∴∠BAC=∠ECB.
∴∠ECB=∠ACO,
∵∠ACO+∠OCB=90°,
∴∠ECB+∠OCB=90°,即CE⊥OC.
∴CE与⊙O相切;
(3)
解:∵CE与⊙O相切,
∴CE2=BEAE,
∵AB=6,CE=4,
∴42=BE(BE+6),
∴BE=2,
∴AE=6+2=8,
∵△ACE∽△CBE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AC=4,
∴AC=CE=4,
∴∠CAB=∠E,
∴∠ECB=∠E,
∴∠ABC=2∠ECB=2∠BAC,BC=BE=2,
∴∠DAB=∠ABC,
∴AD=BC=2.
【解析】(1)①根据圆周角定理即可求得;
②连接OC.欲证明CE是⊙O的切线,只需证明CE⊥OC即可;
(2)根据弦切角定理求得BE,进一步求得AC=4,得出△ACE和△BCE是等腰三角形,得出BC=BE=2,进一步证得∠DAB=∠ABC,从而证得AD=BC=2.


科目:初中数学 来源: 题型:
【题目】 已知△ABC中,∠A=25°,∠B=40°. 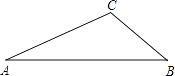
(1)求作:⊙O,使得⊙O经过A、C两点,且圆心O落在AB边上.(要求尺规作图,保留作图痕迹,不必写作法)
(2)求证:BC是(1)中所作⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于体育选考项目统计图
项目 | 频数 | 频率 |
A | 80 | b |
B | c | 0.3 |
C | 20 | 0.1 |
D | 40 | 0.2 |
合计 | a | 1 |
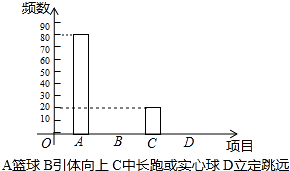
(1)求出表中a,b,c的值,并将条形统计图补充完整. 表中a= , b= , c= .
(2)如果有3万人参加体育选考,会有多少人选择篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4, ![]() ),B(﹣1,2)是一次函数y=kx+b与反比例函数y=
),B(﹣1,2)是一次函数y=kx+b与反比例函数y= ![]() (m≠0,x<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(m≠0,x<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D. 
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图. 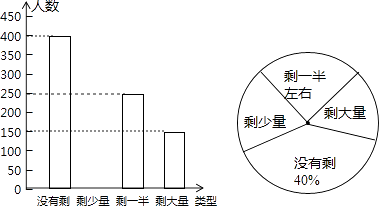
(1)这次被调查的同学共有名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.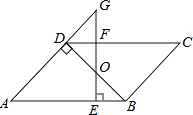
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,P是斜边上一定点,过点P作直线与一直角边交于点Q使图中出现两个相似三角形,这样的点Q有 ( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com