
 如图,分别是吊车在吊一物品时的示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为75°,吊臂AC与地面成75°角.
如图,分别是吊车在吊一物品时的示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为75°,吊臂AC与地面成75°角.分析 (1)欲证明AB=AC,只要证明∠ABC=∠BCA即可.
(2)作AL⊥BC于L,在AE上截取一点M,使得AM=MC.首先证明△ACL≌△ACE,得到CL=CE=2,只要证明∠CME=30°,求出CM,ME即可解决问题.
解答 (1)证明:如图 ,∵∠BCH=30°,∠ACE=75°,
,∵∠BCH=30°,∠ACE=75°,
∴∠ACB=180°-∠BCH-∠ACE=75°,
∵∠ABC=75°,
∴∠ABC=∠BCA,
∴AB=AC.
(2)解:作AL⊥BC于L,在AE上截取一点M,使得AM=MC.
在△ACL和△ACE中,
$\left\{\begin{array}{l}{∠ACL=∠ACE}\\{∠ALC=∠AEC}\\{AC=AC}\end{array}\right.$,
∴△ACL≌△ACE,
∴CL=CE,
∵AB=AC,AL⊥BC,BC=4,
∴BL=CL=CE=2,
∵MA=MC,
∴∠MAC=∠MCA=90°-∠ACE=15°,
∴∠CME=30°,
∴CM=AM=2CE=4,ME=2$\sqrt{3}$,
∴AE=AM+ME=4+2$\sqrt{3}$,
∴AF=AE+EF=4+2$\sqrt{3}$+2=6+2$\sqrt{3}$.
吊车的吊臂顶端A点距地面的高度是(6+2$\sqrt{3}$)米.
点评 本题考查解直角三角形的应用、全等三角形的判定和性质、直角三角形的30度角的性质等知识,解题的关键是灵活运用全等三角形的性质解决问题,学会添加常用辅助线,构造特殊三角形解决问题,属于中考常考题型.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,AD=12cm,CD=8cm,BC=BD=20cm,点P由B出发沿BD方向匀速运动,速度为2cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为2cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题:
如图,在四边形ABCD中,AD∥BC,AD=12cm,CD=8cm,BC=BD=20cm,点P由B出发沿BD方向匀速运动,速度为2cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为2cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 626 | B. | 288 | C. | 168 | D. | 624 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了解某县2014年初中毕业生的实验成绩等级的分布情况,随机抽取了该县若干名学生的实验成绩进行统计分析,并根据抽取的成绩绘制了如图所示的统计图表:
为了解某县2014年初中毕业生的实验成绩等级的分布情况,随机抽取了该县若干名学生的实验成绩进行统计分析,并根据抽取的成绩绘制了如图所示的统计图表:| 成绩等级 | A | B | C | D |
| 人数 | 60 | x | y | 10 |
| 百分比 | 30% | 50% | 15% | m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
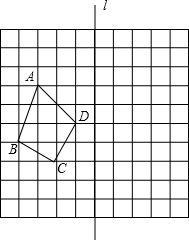 如图,在由边长为1的小正方形组成的10×10的网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.
如图,在由边长为1的小正方形组成的10×10的网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com