
【题目】如图,灯杆AB与墙MN的距离为18米,小丽在离灯杆(底部)9米的D处测得其影长DE为3m,设小丽身高为1.6m.
(1)求灯杆AB的高度;
(2)小丽再向墙走7米,她的影子能否完全落在地面上?若能,求此时的影长;若不能,求落在墙上的影长.

【答案】(1)6.4米;(2)不能完全落在地面上,落在墙上的影长为1米
【解析】试题分析:(1)由相似三角形对应成比例即可求出AB的长.
(2)假设全部在地上,设影长为x,同样求出影长x,而9+7+影长>18.故有部分影子落在墙上.超过的影长,相当于墙上影长在地上的投影,设落在墙上的影长为y,则有y:6.4=![]() :(
:(![]() +18),求出y的值即可.
+18),求出y的值即可.
试题解析:解:(1)∵AB∥CD,∴△CDE∽△ABE,∴CD:AB=DE:BE,∴1.6:AB=3:12,解得:AB=6.4.
答:灯杆AB的高度为6.4米.
(2)假设全部在地上,设影长为x,则CD:AB=DE:BE,∴1.6:6.4=x:(9+7+x),解得:x=![]() ,而9+7+
,而9+7+![]() -18=
-18=![]() >0.故有部分影子落在墙上.
>0.故有部分影子落在墙上.
因为超过的影长为![]() ,相当于墙上影长在地上的投影,故设落在墙上的影长为y,则有y:6.4=
,相当于墙上影长在地上的投影,故设落在墙上的影长为y,则有y:6.4=![]() :(
:(![]() +18),解得:y=1.故落在墙上的影子长为1米.
+18),解得:y=1.故落在墙上的影子长为1米.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图(1),AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图(2),∠BDC的平分线分别交AC,BC于点E,F,求∠CEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若甲组数据的方差比乙组数据的方差大,那么下列说法正确的是( )
A.甲组数据的平均数比乙组数据的平均数大
B.甲组数据比乙组数据稳定
C.乙组数据比甲组数据稳定
D.甲、乙组的稳定性不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列4个命题:①相等的角是对顶角;②互补的两个角中一定是一个为锐角,另一个为钝角;③平行于同一条直线的两条直线平行;④同位角相等.其中真命题的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A.打开电视机正在播放广告
B.投掷一枚质地均匀的硬币100次,正面向上的次数为50次
C.任意一个一元二次方程都有实数根
D.在平面上任意画一个三角形,其内角和是180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校把学生学科的期中、期末两次成绩分别按40%,60%的比例计入学期学科总成绩.小明期中数学成绩是85分,期末数学总成绩是90分,那么他的学期数学成绩( )
A. 85分 B. 87.5分 C. 88分 D. 90分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,一次函数y=﹣![]() x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.
x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.

(1)若直线AB与![]() 有两个交点F、G.
有两个交点F、G.
①求∠CFE的度数;
②用含b的代数式表示FG2,并直接写出b的取值范围;
(2)设b≥5,在线段AB上是否存在点P,使∠CPE=45°?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
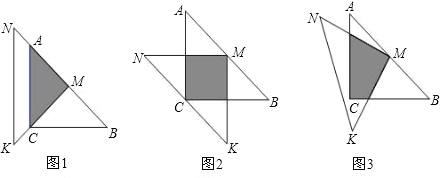
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为 ,周长为 .
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 ,周长为 .
2(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com