
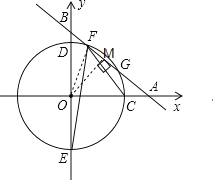
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕxOyжаЃЌвЛДЮКЏЪ§y=Љ![]() x+bЃЈbЮЊГЃЪ§ЃЌbЃО0ЃЉЕФЭМЯѓгыxжсЁЂyжсЗжБ№ЯрНЛгкЕуAЁЂBЃЌАыОЖЮЊ4ЕФЁбOгыxжсе§АыжсЯрНЛгкЕуCЃЌгыyжсЯрНЛгкЕуDЁЂEЃЌЕуDдкЕуEЩЯЗНЃЎ
x+bЃЈbЮЊГЃЪ§ЃЌbЃО0ЃЉЕФЭМЯѓгыxжсЁЂyжсЗжБ№ЯрНЛгкЕуAЁЂBЃЌАыОЖЮЊ4ЕФЁбOгыxжсе§АыжсЯрНЛгкЕуCЃЌгыyжсЯрНЛгкЕуDЁЂEЃЌЕуDдкЕуEЩЯЗНЃЎ

ЃЈ1ЃЉШєжБЯпABгы![]() гаСНИіНЛЕуFЁЂGЃЎ
гаСНИіНЛЕуFЁЂGЃЎ
ЂйЧѓЁЯCFEЕФЖШЪ§ЃЛ
ЂкгУКЌbЕФДњЪ§ЪНБэЪОFG2ЃЌВЂжБНгаДГіbЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЩшbЁн5ЃЌдкЯпЖЮABЩЯЪЧЗёДцдкЕуPЃЌЪЙЁЯCPE=45ЁуЃПШєДцдкЃЌЧыЧѓГіPЕузјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ45ЁуЃЛЃЈ2ЃЉ4ЁмbЃМ5ЃЛЃЈ3ЃЉДцдк PЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЂйЁЯEOCКЭЁЯEFCЪЧ![]() ЫљЖдЕФдВаФНЧКЭдВжмНЧЃЌИљОнЭЌЛЁЫљЖдЕФдВжмНЧЪЧдВаФНЧЕФвЛАыНјааЧѓНтМДПЩЃЛ
ЫљЖдЕФдВаФНЧКЭдВжмНЧЃЌИљОнЭЌЛЁЫљЖдЕФдВжмНЧЪЧдВаФНЧЕФвЛАыНјааЧѓНтМДПЩЃЛ
ЂкЙ§OзїOMЁЭFGгкЕуMЃЌСЌНгOFЃЌЯШЧѓГівЛДЮКЏЪ§ЭМЯёгыxжсЁЂyжсНЛЕуAЁЂBЕФзјБъЃЌШЛКѓИљОнЙДЙЩЖЈРэЧѓГіABЕФГЄЃЌНјЖјРћгУУцЛ§ЗЈЧѓГіOMЕФГЄЃЌдйРћгУЙДЙЩЖЈРэБэЪОГіFM2ЃЌдйгЩДЙОЖЖЈРэЕУFGЃН2FMЃЌНјЖјПЩвдБэЪОГіFG2ЃЌдйИљОнЪНзгаДГіbЕФЗЖЮЇЃЛ
ЃЈ2ЃЉИљОнЧАУцНсТлOMЃН![]() ЃЌЕБbЃО5ЪБЃЌжБЯпгыдВЯрРыЃЌЕБbЃН5ЪБЃЌжБЯпгыдВЯрЧаЃЌСЌНгOPЃЌИљОнСНжБЯпДЙжБЪББШР§ЯЕЪ§ЕФЛ§ЮЊЃ1ЧѓГіOPЕФНтЮіЪНЃЌШЛКѓСЊСЂСНИіНтЮіЪНМДПЩЧѓГіЕуPЕФзјБъЃЎ
ЃЌЕБbЃО5ЪБЃЌжБЯпгыдВЯрРыЃЌЕБbЃН5ЪБЃЌжБЯпгыдВЯрЧаЃЌСЌНгOPЃЌИљОнСНжБЯпДЙжБЪББШР§ЯЕЪ§ЕФЛ§ЮЊЃ1ЧѓГіOPЕФНтЮіЪНЃЌШЛКѓСЊСЂСНИіНтЮіЪНМДПЩЧѓГіЕуPЕФзјБъЃЎ
ЪдЬтНтЮіЃК
НтЃКЃЈ1ЃЉЂйЁпЁЯCOEЃН90ЁуЃЌ
ЁрЁЯCFEЃН![]() ЁЯCOEЃН45ЁуЃЛ
ЁЯCOEЃН45ЁуЃЛ
ЂкШчЭМЃЌзїOMЁЭABЕуMЃЌСЌНгOFЃЌ
ЁпжБЯпЕФКЏЪ§ЪНЮЊЃКyЃН![]() ЃЌ
ЃЌ
ЁрBЕФзјБъЮЊЃЈ0ЃЌbЃЉЃЌAЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЁрABЃН![]()
ЃН![]() ЃЌ
ЃЌ
дкRtЁїOBCжаЃЌгЩУцЛ§ЗЈПЩЕУ
OAЁЄOBЃНABЁЄOMЃЌ
взЕУЃКOMЃН![]() ЃЌ
ЃЌ
ЁпOFЃН4ЃЌ
ЁрFM2ЃНOF2ЉOM2ЃН42ЉЃЈ![]() ЃЉ2 ЃЌ
ЃЉ2 ЃЌ
ЁпOMЁЭFGЃЌ
ЁрFGЃН2FMЃЌ
ЁрFG2ЃН4FM2ЃН4ЁС[42ЉЃЈ![]() ЃЉ2 ]ЃН64Љ
ЃЉ2 ]ЃН64Љ![]() b2ЃЌ
b2ЃЌ
ЁпжБЯпABгы![]() гаСНИіНЛЕуFЁЂGЃЎ
гаСНИіНЛЕуFЁЂGЃЎ
Ёр4ЁмbЃМ5ЃЛ
ЃЈ2ЃЉДцдкЃЎ
ШчЭМЃЌ
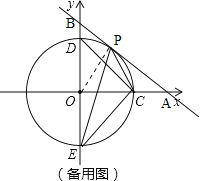
ЕБbЃО5ЪБЃЌOMЃН![]() ЃО4ЃЌЁржБЯпгыдВЯрРыЃЌЁЯCPEЃМ45ЁуЃЛ
ЃО4ЃЌЁржБЯпгыдВЯрРыЃЌЁЯCPEЃМ45ЁуЃЛ
ЕБbЃН5ЪБЃЌOMЃН![]() ЃН4ЃЌЁржБЯпгыдВЯрЧаЃЌ
ЃН4ЃЌЁржБЯпгыдВЯрЧаЃЌ
ЁпDEЪЧжБОЖЃЌ
ЁрЁЯDCEЃН90ЁуЃЌ
ЁпCOЁЭDEЃЌЧвDOЃНEOЃЌ
ЁрЁЯODCЃНЁЯOECЃН45ЁуЃЌ
ЁрЁЯCPEЃНЁЯODCЃН45ЁуЃЌ
ЁрДцдкЕуPЃЌЪЙЁЯCPEЃН45ЁуЃЌ
СЌНгOPЃЌ
ЁпPЪЧЧаЕуЃЌЁрOPЁЭABЃЌЁрOPЫљдкЕФжБЯпЮЊЃКyЃН![]() ЃЌ
ЃЌ
гжЁпABЫљдкЕФжБЯпЮЊЃКyЃН![]() ЃЋ5ЃЌ
ЃЋ5ЃЌ
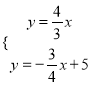
НтЕУ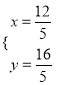
ЁрPЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЙигкСтаЮЁЂОиаЮЕФЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A.СтаЮЕФЖдНЧЯпЯрЕШЧвЛЅЯрЦНЗж
B.ОиаЮЕФЖдНЧЯпЯрЕШЧвЛЅЯрЦНЗж
C.ЖдНЧЯпЛЅЯрДЙжБЕФЫФБпаЮЪЧСтаЮ
D.ЖдНЧЯпЯрЕШЕФЫФБпаЮЪЧОиаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕЦИЫABгыЧНMNЕФОрРыЮЊ18УзЃЌаЁРідкРыЕЦИЫЃЈЕзВПЃЉ9УзЕФDДІВтЕУЦфгАГЄDEЮЊ3mЃЌЩшаЁРіЩэИпЮЊ1.6m.
ЃЈ1ЃЉЧѓЕЦИЫABЕФИпЖШЃЛ
ЃЈ2ЃЉаЁРідйЯђЧНзп7УзЃЌЫ§ЕФгАзгФмЗёЭъШЋТфдкЕиУцЩЯЃПШєФмЃЌЧѓДЫЪБЕФгАГЄЃЛШєВЛФмЃЌЧѓТфдкЧНЩЯЕФгАГЄ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁбAгыyжсЯрЧагкдЕуOЃЌЦНаагкxжсЕФжБЯпНЛЁбAгкMЁЂMСНЕуЃЌШєЕуMЕФзјБъЪЧЃЈ-4ЃЌ-2ЃЉЃЌдђЕуNЕФзјБъЮЊЃЈ ЃЉ

AЃЎЃЈ-1ЃЌ-2ЃЉ BЃЎЃЈ1ЃЌ2ЃЉ CЃЎЃЈ-1ЃЎ5ЃЌ-2ЃЉ DЃЎЃЈ1ЃЎ5ЃЌ-2ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП МзЁЂввСНЬЈАќзАЛњЭЌЪБАќзАжЪСПЮЊ500ПЫЕФЬЧЙћЃЌДгжаИїГщГі10ДќЃЌВтЕУЦфЪЕМЪжЪСПЗжБ№ШчЯТ(ЕЅЮЛЃКПЫ)ЃК
Мз 501 500 508 506 510 509 500 493 494 494
вв 503 504 502 496 499 501 505 497 502 499
ФФЬЈАќзАЛњАќзАЕФ10ДќЬЧЙћЕФжЪСПБШНЯЮШЖЈЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОнЭГМЦЃЌгхББЧјЕкЖўНьЁАбЖЗЩБЁБгХжЪПЮДѓШќЪгЦЕЭјТчЕуЛї 10500 ДЮЃЌНЋЪ§ 10500 гУПЦбЇМЧЪ§ЗЈБэЪОЮЊЃЈ ЃЉ
A. 10.5105B. 1.05105C. 0.105105D. 1.05104
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКўФЯЕиЭМГіАцЩчЪзЗЂЕФЪњАцЁЖжаЛЊШЫУёЙВКЭЙњЕиЭМЁЗЃЌНЋФЯКЃжюЕКгыжаЙњДѓТНАДЭЌБШР§Гп1ЃК6700000БэЪОГіРДЃЌЪЙЖСепФмЙЛШЋУцЁЂжБЙлЕиШЯЪЖЮвЙњАцЭМЃЌШєдкетжжЕиЭМЩЯСПЕУЮвЙњФЯББЕФЭМЩЯОрРыЪЧ82.09РхУзЃЌдђЮвЙњФЯББЕФЪЕМЪОрРыДѓдМЪЧЧЇУзЃЈНсЙћОЋШЗЕН1ЧЇУзЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвдMЃЈ0ЃЌ2ЃЉдВаФЃЌ4ЮЊАыОЖЕФЁбMНЛxжсгкAЁЂBСНЕуЃЌНЛyжсгкCЁЂDСНЕуЃЌСЌНсBMВЂбгГЄНЛЁбMгкЕуPЃЌСЌНсPCНЛxжсгкЕуEЃЎ
ЃЈ1ЃЉЧѓЁЯDMPЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЧѓЁїBPEЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com