
【题目】如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1.求证:AD平分∠BAC.
下面是部分推理过程,请你将其补充完整:
∵AD⊥BC于D,EG⊥BC于G (已知)
∴∠ADC=∠EGC=90°
∴AD∥EG .
∴∠1=∠2 .
=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3 .
∴AD平分∠BAC . 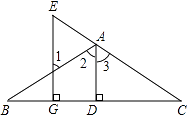
【答案】同位角相等,两直线平行;两直线平行,内错角相等;∠E;等量代换;角平分线的定义
【解析】解:∵AD⊥BC于D,EG⊥BC于G (已知)
∴∠ADC=∠EGC=90°
∴AD∥EG,(同位角相等,两直线平行).
∴∠1=∠2,(两直线平行,内错角相等).
∠E=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3,(等量代换).
∴AD平分∠BAC.(角平分线的定义)
所以答案是:同位角相等,两直线平行;两直线平行,内错角相等;∠E;等量代换;角平分线的定义.
【考点精析】掌握垂线的性质和平行线的判定与性质是解答本题的根本,需要知道垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
【题目】判断下列几组选取样本的方法是否合适:
(1)小丽想了解某市中学生晚上在家复习功课的时间,调查了她所在学校九年级的50名同学;
(2)苗苗想了解她所在学校的学生课外阅读名著的情况,随机调查了该校50名同学;
(3)某电视台需要了解某个节目的收视率,对一所大学的学生进行了调查.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AD是∠BAC的平分线,若AB=AC+CD,那么∠ACB与∠ABC有怎样的数量关系?小明通过观察分析,形成了如下解题思路: 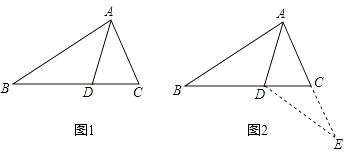
如图2,延长AC到E,使CE=CD,连接DE.由AB=AC+CD,可得AE=AB.又因为AD是∠BAC的平分线,可得△ABD≌△AED,进一步分析就可以得到∠ACB与∠ABC的数量关系.
(1)判定△ABD与△AED全等的依据是;
(2)∠ACB与∠ABC的数量关系为: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com