练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】(－2x2)3·(x2＋x2y2＋y2)的结果中次数是10的项的系数是________．

    【答案】-8

    【解析】

    （-2x2）3（x2+x2y2+y2）=-8x6（x2+x2y2+y2）=-8x8-8x8y2-8x6y2，次数是10的项是-8x8y2，系数是-8．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，一枚质地均匀的正四面体骰子，它有四个面并分别标有数字，，，，如图，正方形顶点处各有一个圈．跳圈游戏的规则为：游戏者每掷一次骰子，骰子着地一面上的数字是几，就沿正方形的边顺时针方向连续跳几个边长．如：若从图起跳，第一次掷得，就顺时针连续跳个边长，落到圈；若第二次掷得，就从开始顺时针连续跳个边长，落到圈；设游戏者从圈起跳．

    （）嘉嘉随机掷一次骰子，求落回到圈的概率．

    （）淇淇随机掷两次骰子，用列表法求最后落回到圈的概率，并指出她与嘉嘉落回到圈的可能性一样吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用科学记数法表示﹣0.000000059= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各数中，不是不等式2-3x＞5的解的是（ ）

    A. -2 B. -3 C. -1 D. -1.35

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，过点A（2，0）的两条直线l1 ， l2分别交y轴于点B，C，其中点B在原点上方，点C在原点下方，已知AB= ．
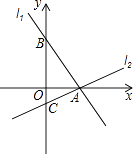
    （1）求点B的坐标；
    （2）若△ABC的面积为4，求直线l2的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，记直线y=x+1为l．点A1是直线l与y轴的交点，以A1O为边作正方形A1OC1B1，使点C1落在在x轴正半轴上，作射线C1B1交直线l于点A2，以A2C1为边作正方形A2C1C2B2，使点C2落在在x轴正半轴上，依次作下去，得到如图所示的图形．则点B4的坐标是 ，点Bn的坐标是 ．

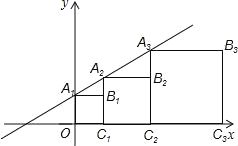
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛，若圆形的半径为r米，广场长为a米，宽为b米．

    （1）请列式表示广场空地的面积；
    （2）若休闲广场的长为400米，宽为100米，圆形花坛的半径为10米，求广场空地的面积（计算结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解答
    （1）如图1，小明和小亮在研究一个数学问题：已知AB∥CD，AB和CD都不经过点P，探索∠P与∠A，∠C的数量关系．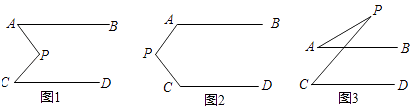

    小明是这样证明的：过点P作PQ∥AB
    ∴∠APQ=∠A（）
    ∵PQ∥AB，AB∥CD．
    ∴PQ∥CD（）
    ∴∠CPQ=∠C
    ∴∠APQ+∠CPQ=∠A+∠C
    即∠APC=∠A+∠C
    小亮是这样证明的：过点作PQ∥AB∥CD．
    ∴∠APQ=∠A，∠CPQ=∠C
    ∴∠APQ+∠CPQ=∠A+∠C
    即∠APC=∠A+∠C
    请在上面证明过程的过程的横线上，填写依据；两人的证明过程中，完全正确的是 ．
    （2）应用：
    在图2中，若∠A=120°，∠C=140°，则∠APC的度数为；
    （3）拓展：
    在图3中，探索∠APC与∠A，∠C的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：AD⊥BC于D，EG⊥BC于G，∠E=∠1．求证：AD平分∠BAC．
    下面是部分推理过程，请你将其补充完整：
    ∵AD⊥BC于D，EG⊥BC于G （已知）
    ∴∠ADC=∠EGC=90°
    ∴AD∥EG ．
    ∴∠1=∠2 ．
    =∠3（两直线平行，同位角相等）
    又∵∠E=∠1（已知）
    ∴∠2=∠3 ．
    ∴AD平分∠BAC ．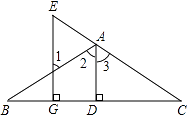

    查看答案和解析>>

    同步练习册答案