
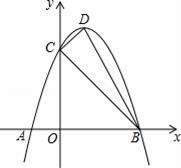
如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
(1)求抛物线解析式;
(2)求证:△BCD为直角三角形;
(3)在x轴上方的抛物线上,是否存在点M,过M作MN⊥x轴于N点,使△BMN与△BCD相似?若存在,请求出M的坐标;若不存在,请说明理由.


【考点】二次函数综合题.
【分析】(1)将x=0代入可求得y=3,故此可知C(0,3),OC=3,OA=1,则点A的坐标为(﹣1,0),由点B与点A关于x=1对称可知B(3,0),将点A、点B的坐标代入抛物线的解析式,从而求得a=﹣1,b=2;
(2)先利用配方法求出抛物线的顶点D的坐标,再利用两点间的距离公式得出CD2+BC2=BD2,由勾股定理的逆定理即可证明△BCD为直角三角形;
(3)由(2)知,CD=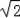
 ,BC=
,BC=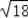
 =3
=3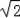
 .设M(x,﹣x2+2x+3),则MN=﹣x2+2x+3,BN=3﹣x,由于∠MNB=∠BCD=90°,所以当△BMN与△BCD相似时,分两种情况:①△BMN∽△BDC;②△BMN∽△DBC.然后根据相似三角形的性质列出关于x的方程,从而求得点M的坐标.
.设M(x,﹣x2+2x+3),则MN=﹣x2+2x+3,BN=3﹣x,由于∠MNB=∠BCD=90°,所以当△BMN与△BCD相似时,分两种情况:①△BMN∽△BDC;②△BMN∽△DBC.然后根据相似三角形的性质列出关于x的方程,从而求得点M的坐标.
【解答】解:(1)∵将x=0代入y=ax2+bx+3,得y=3,
∴C(0,3).
∵OC=3OA,
∴OA=1,
∴A(﹣1,0).
∵点B与点A关于x=1对称,
∴B(3,0).
将A(﹣1,0),B(3,0)代入y=ax2+bx+3得:

 ,
,
解得: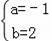
 .
.
∴抛物线解析式为y=﹣x2+2x+3;
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D的坐标为(1,4).
∵A(﹣1,0),B(3,0),C(0,3),
∴CD2=(1﹣0)2+(4﹣3)2=2,
BC2=(3﹣0)2+(0﹣3)2=18,
BD2=(1﹣3)2+(4﹣0)2=20,
∴CD2+BC2=BD2,
∴△BCD为直角三角形;
(3)由(2)知,CD=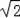
 ,BC=
,BC=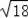
 =3
=3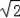
 .
.
设在x轴上方的抛物线上存在点M(x,﹣x2+2x+3),则﹣1<x<3,﹣x2+2x+3>0,
∵MN⊥x轴于N点,
∴N(x,0),∠MNB=90°,
∴BN=3﹣x,MN=﹣x2+2x+3.
∵Rt△BCD中,∠BCD=90°,
∴∠MNB=∠BCD=90°,
∴当△BMN与△BCD相似时,分两种情况:
①如果△BMN∽△BDC,那么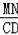
 =
=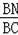
 ,
,
即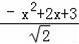
 =
=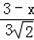
 ,
,
解得x1=3,x2=﹣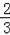
 ,
,
又∵﹣1<x<3,
∴x=﹣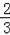
 ,
,
∴﹣x2+2x+3=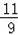
 ,
,
∴M(﹣
 ,
,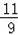
 );
);
②如果△BMN∽△DBC,那么
 =
=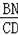
 ,
,
即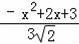
 =
=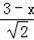
 ,
,
解得x1=2,x2=3,
又∵﹣1<x<3,
∴x=2,
∴﹣x2+2x+3=3,
∴M(2,3).
综上所述,M点坐标为(﹣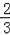
 ,
,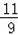
 )或(2,3).
)或(2,3).

【点评】本题是二次函数综合题,其中涉及到利用待定系数法求二次函数的解析式、二次函数的性质、两点间的距离公式、勾股定理的逆定理、相似三角形的性质等知识点,利用分类讨论、数形结合与方程思想是解题的关键.


科目:初中数学 来源: 题型:
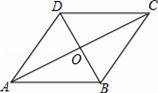
如图,在▱ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB.
(1)求证:四边形ABCD为菱形;
(2)若AB=12,∠DAB=60°,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
绵阳市“全国文明村”江油白玉村果农王灿收获枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)王灿如何安排甲、乙两种货车可一次性地运到销售地有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王灿应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com