
【题目】如图,已知直线y1=![]() x与双曲线y2=
x与双曲线y2=![]() (k>0)交于A、B两点,且点A的横坐标为4.
(k>0)交于A、B两点,且点A的横坐标为4.
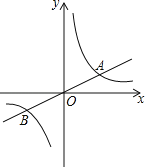
(1)k的值为 ;当x的取值范围为 时,y1>y2;
(2)若双曲线y2=![]() (k>0)上一点C的纵坐标为8,求△AOC的面积.
(k>0)上一点C的纵坐标为8,求△AOC的面积.
【答案】(1)8、x>4或﹣4<x<0(2)15
【解析】
试题分析:(1)根据正比例函数先求出点A的坐标,从而求出了k值为8,然后通过解方程组求得B的坐标,根据图象即可求得y1>y2时的x的取值.;
(2)过A、C点分别作x轴、y轴的垂线垂足为G、E,两垂线交于点F,则四边形EFGO是矩形,根据C的纵坐标求得C的坐标,然后根据S△AOC=S矩形﹣SOEC﹣S△CFA﹣S△OAG计算即可.
解:(1)∵点A横坐标为4,
∴由y1=![]() x可知当x=4时,y=2.
x可知当x=4时,y=2.
∴点A的坐标为(4,2).
∵点A是直线y1=![]() x与双曲线y2=
x与双曲线y2=![]() (k>0)的交点,
(k>0)的交点,
∴k=4×2=8.
∴双曲线的解析式为y=![]() ,
,
解![]() 得
得![]() 或
或![]() ,
,
∴A((4,2),B(﹣4,﹣2),
根据图象可知:当x>4或﹣4<x<0时,y1>y2;
故答案为8、x>4或﹣4<x<0.
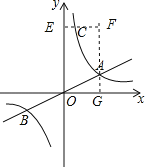
(2)如图,过A、C点分别作x轴、y轴的垂线垂足为G、E,两垂线交于点F,则四边形EFGO是矩形,
∵点C在双曲线上,点C的纵坐标为8,
∴8=![]() ,解得x=1,
,解得x=1,
∴C(1,8),
∴S△AOC=S矩形﹣SOEC﹣S△CFA﹣S△OAG=8×4﹣![]() ×1×8﹣
×1×8﹣![]() (4﹣1)×(8﹣2)﹣
(4﹣1)×(8﹣2)﹣![]() ×4×2=32﹣4﹣9﹣4=15.
×4×2=32﹣4﹣9﹣4=15.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
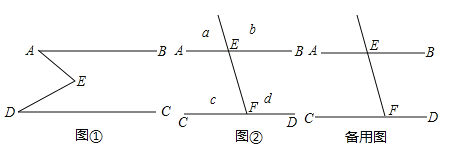
【题目】如图①,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=20°,∠D=40°,则∠AED= °
②猜想图①中∠AED,∠EAB,∠EDC的关系,并用两种不同的方法证明你的结论.
(2)拓展应用:
如图②,射线FE与l1,l2交于分别交于点E、F,AB∥CD,a,b,c,d分别是被射线FE隔开的4个区域(不含边界,其中区域a,b位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(任写出两种,可直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有甲、乙两个构造完全相同的转盘均被分成A、B两个区域,甲转盘中A区域的圆心角是120°,乙转盘A区域的圆心角是90°,自由转动转盘,如果指针指向区域分界线则重新转动.
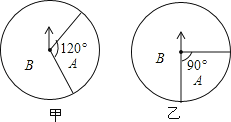
(1)转动甲转盘一次,则指针指向A区域的概率 ;
(2)自由转动两个转盘各一次,请用树状图或列表的方法,求出两个转盘同时指向B区域的概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com