

分析 (1)观察不难发现,后一个图形比前一个图形多3个小正方形,1个大正方形,然后根据全三个图形的正方形的个数的规律写出第n个图形中正方形的个数,再把n=6代入公式进行计算即可得解;
(2)把正方形的个数7999代入公式进行计算即可得解.
解答 解:(1)第1个图形有3个正方形,3=4×1-1,
第2个图形有7个正方形,7=4×2-1,
第3个图形有11个正方形,11=4×3-1,
…,
依此类推,第n个图形有4n-1个正方形;
当n=6时,4×6-1=23;
(2)∵4n-1=7999,
∴n=2000.
故答案为:23,2000.
点评 此题考查图形的变化规律,观察出后一个图形比前一个图形多4个正方形,从而写出第n个图形的正方形的个数是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | -4ab2+2 | B. | -2ab2-8 | C. | 4a2b-2ab2+2 | D. | 4ab2-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
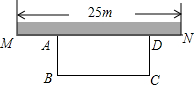 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可供利用25m),现在已备足可以砌50m长的墙的材料.
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可供利用25m),现在已备足可以砌50m长的墙的材料.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com