
����Ŀ��ij�������۹�˾һλ���۾���1~5�·ݵ���������ͳ��ͼ����(����ͳ��ͼ��������)��
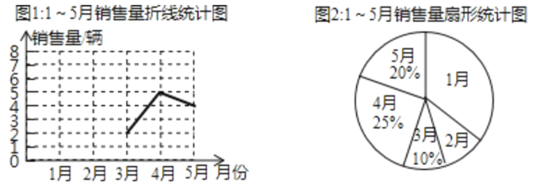
�����ͼ����Ϣ�������������:
��1����1�µ���������2�µ���������![]() ������ȫͼ1������������ͳ��ͼ��
������ȫͼ1������������ͳ��ͼ��
��2����ͼ2�У�2�µ�����������Ӧ�����ε�Բ�ĽǴ�СΪ ![]() ��
��
��3���ݴ˹��㱾����������۵������Ƕ��٣�
��4����֪5�·����۵ij�����![]() ����������
����������![]() �����ʳ����������ֱ���
�����ʳ����������ֱ���![]() ��ʾ�����ʳ��ֱ���
��ʾ�����ʳ��ֱ���![]() ��ʾ���ִ���
��ʾ���ִ���![]() �����������ȡ�������μӹ�˾�Ļ���������û���״ͼ���б�����������鵽�����������ǹ��������ĸ��ʣ�
�����������ȡ�������μӹ�˾�Ļ���������û���״ͼ���б�����������鵽�����������ǹ��������ĸ��ʣ�
���𰸡���1�������������2��36����3��48����4��![]()
��������
��1�������1~5�·ݵ�������������������2�µ�������Ϊx����������õ����̹ʿ���⣻
��2�������2�µ�������ռ1~5�·ݵ��������������İٷֱȣ��ٳ���360�㼴����⣻
��3�����1~5�·ݵ���������ƽ��ֵ���ٳ���12������⣻
��4���������⻭����״ͼ���ٸ��ݸ��ʹ�ʽ������⣮
��1����ͳ��ͼ�ɵ�3�·ݵ�������Ϊ2����ռ��Ϊ10%��
��1~5�·ݵ�������������Ϊ2��10%=20����
��2�µ�������Ϊx������1�µ�������3.5x����
��3.5x+x+2+5+4=20��
���x=2��
�����飬�������⣬
��1�µ�������7����2�µ�������Ϊ2����
��ȫͼ1������������ͳ��ͼ���£�
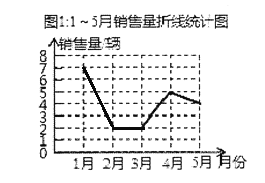
��2��2�µ�����������Ӧ�����ε�Բ�ĽǴ�СΪ2��20��360��=36����
��3��1~5�·ݵ���������ƽ��ֵΪ![]() ��������
��������
����㱾����������۵�������4��12=48����
��4�������⻭��״ͼ���£�
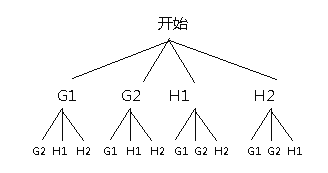
��P���鵽�����������ǹ�������=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
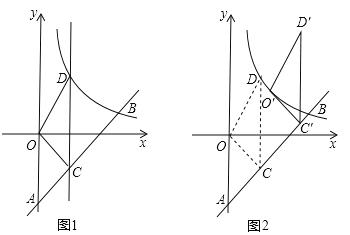
����Ŀ����2016����ʡ���У� ��2016����ͼ1��һ�κ���y=kx��3��k��0����ͼ����y�ύ�ڵ�A���뷴��������![]() ��x��0����ͼ���ڵ�B��4��b����
��x��0����ͼ���ڵ�B��4��b����
��1��b= ��k= ��
��2����C���߶�AB�ϵĶ��㣨�ڵ�A��B���غϣ�������C��ƽ����y���ֱ��l�����������������ͼ���ڵ�D������OCD��������ֵ��
��3������2�������ȡ�����ֵ����OCD������AB����ƽ��һ���ľ��룬�õ���O��C��D��������O�Ķ�Ӧ��O�����ڸ÷���������ͼ���ϣ���ͼ2�������D���������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
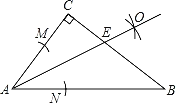
����Ŀ����ͼ��ʾ����Rt��ABC�У���C��90���������²�����ͼ��
���Ե�AΪԲ�ģ���С��AC�ij�Ϊ�뾶�������ֱ�AC��AB�ڵ�M��N��
�ڷֱ��Ե�M��NΪԲ�ģ��Դ���![]() MN�ij�Ϊ�뾶�����������ཻ�ڵ�O��
MN�ij�Ϊ�뾶�����������ཻ�ڵ�O��
��������OA����BC�ڵ�E����CE��6��BE��10��
��AB�ij���������
A.11B.12C.18D.20
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣����ϱ������ɽ·�붫����ı���·��������ֱ�ߣ�ʮ��·�ڼ�����![]() ���״���ɽ·�ϵ�
���״���ɽ·�ϵ�![]() �������ﳵ������ֱ�У����ͬʱ���Ҵӵ�
�������ﳵ������ֱ�У����ͬʱ���Ҵӵ�![]() �������ر���·����������ֱ�У������
�������ر���·����������ֱ�У������![]() ʱ���ס����������
ʱ���ס����������![]() �ľ���ֱ�Ϊ
�ľ���ֱ�Ϊ![]() ��
��![]() ����֪
����֪![]() ��
��![]() ��
��![]() ֮��ĺ�����ϵ��ͼ����ʾ��
֮��ĺ�����ϵ��ͼ����ʾ��
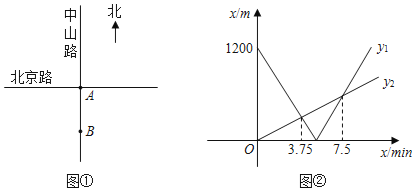
��1����ס������˵��ٶȣ�
��2����![]() ȡ��ֵʱ���ס�������֮��ľ�����̣�
ȡ��ֵʱ���ס�������֮��ľ�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������CD��AB�ڵ�E����F����O��һ�㣬��![]() ��
��![]() ������FB��FD��FD��AB�ڵ�N��
������FB��FD��FD��AB�ڵ�N��
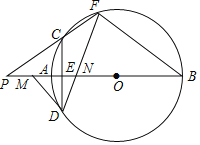
��1����AE��1��CD��6������O�İ뾶��
��2����֤����BNFΪ���������Σ�
��3������FC���ӳ�����BA���ӳ����ڵ�P������D����O�����ߣ���BA���ӳ����ڵ�M����֤��ONOP��OEOM��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪���ı���ABCD�У�![]() ��
��![]() ��
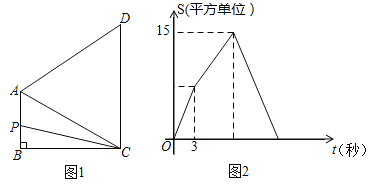
��![]() ������P�ӵ�B����������B��A��D��C�ķ�����1����λ/����ٶ������˶��������˶������У���BCP�����S���˶�ʱ��t���룩�ĺ�����ϵ��ͼ2��ʾ����AD�ij�Ϊ�� ��
������P�ӵ�B����������B��A��D��C�ķ�����1����λ/����ٶ������˶��������˶������У���BCP�����S���˶�ʱ��t���룩�ĺ�����ϵ��ͼ2��ʾ����AD�ij�Ϊ�� ��
A.5B.![]() C.8D.
C.8D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���ABCD�У�AB��6��BC��8����E�DZ�CD�ϵĵ㣬��CE��4������E��CD�Ĵ��ߣ����ڴ����Ͻ�ȡEF��3������CF������CEF�Ƶ�C��˳ʱ�뷽����ת������ת��Ϊa��
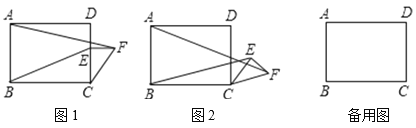
��1�����ⷢ��
��a��0��ʱ��AF�� ��BE�� ��![]() �� ��
�� ��
��2����չ̽��
���жϣ���0���a����360��ʱ��![]() �Ĵ�С���ޱ仯�������ͼ2���������֤����
�Ĵ�С���ޱ仯�������ͼ2���������֤����
��3��������
����CEF��ת��A��E��F���㹲��ʱ��ֱ��д���߶�BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�����ı���ABCD�У�AB��AC��DC��AC����B=��D��![]() ��
��![]() ��
��![]() ����E��F�ֱ���BC��AD���е㣮
����E��F�ֱ���BC��AD���е㣮
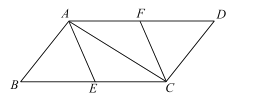
��1����֤��![]() ��
��
��2����![]() ��
��![]() ����ʲô������ϵʱ���ı���
����ʲô������ϵʱ���ı���![]() �������Σ���֤����
�������Σ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ھ�������һ�����μ���Ʒ����֪ÿ������Ϊ![]() Ԫ�������۵��۶�Ϊ
Ԫ�������۵��۶�Ϊ![]() Ԫʱ��ÿ���������
Ԫʱ��ÿ���������![]() �����г����鷴ӳ�����۵���ÿ���
�����г����鷴ӳ�����۵���ÿ���![]() Ԫ���������������
Ԫ���������������![]() ������۲��Ź涨�����۵��۲��ܳ���
������۲��Ź涨�����۵��۲��ܳ���![]() Ԫ�������۵���Ϊ
Ԫ�������۵���Ϊ![]() (Ԫ)��
(Ԫ)��
��1��Ҫʹ����������Ϊ![]() Ԫ�����۵���Ӧ��Ϊ����Ԫ��
Ԫ�����۵���Ӧ��Ϊ����Ԫ��
��2��������������![]() (Ԫ)�����۵���
(Ԫ)�����۵���![]() (Ԫ)�ĺ�����ϵʽ����
(Ԫ)�ĺ�����ϵʽ����![]() Ϊ��ֵʱ�������������������������
Ϊ��ֵʱ�������������������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com