
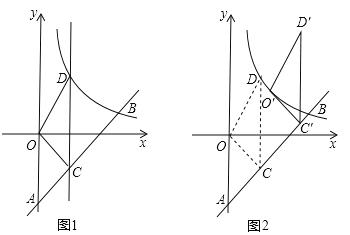
【题目】(2016江苏省镇江市) (2016镇江)如图1,一次函数y=kx﹣3(k≠0)的图象与y轴交于点A,与反比例函数![]() (x>0)的图象交于点B(4,b).
(x>0)的图象交于点B(4,b).
(1)b= ;k= ;
(2)点C是线段AB上的动点(于点A、B不重合),过点C且平行于y轴的直线l交这个反比例函数的图象于点D,求△OCD面积的最大值;
(3)将(2)中面积取得最大值的△OCD沿射线AB方向平移一定的距离,得到△O′C′D′,若点O的对应点O′落在该反比例函数图象上(如图2),则点D′的坐标是 .
【答案】(1)1,1;(2)![]() ;(3)D′(
;(3)D′(![]() ,
,![]() ).
).
【解析】试题(1)由点B的横坐标利用反比例函数图象上点的坐标特征即可求出b值,进而得出点B的坐标,再将点B的坐标代入一次函数解析式中即可求出k值;
(2)设C(m,m﹣3)(0<m<4),则D(m,![]() ),根据三角形的面积即可得出S△OCD关于m的函数关系式,通过配方即可得出△OCD面积的最大值;
),根据三角形的面积即可得出S△OCD关于m的函数关系式,通过配方即可得出△OCD面积的最大值;
(3)由(1)(2)可知一次函数的解析式以及点C、D的坐标,设点C′(a,a﹣3),根据平移的性质找出点O′、D′的坐标,由点O′在反比例函数图象上即可得出关于a的方程,解方程求出a的值,将其代入点D′的坐标中即可得出结论.
试题解析:解:(1)把B(4,b)代入![]() (x>0)中得:b=
(x>0)中得:b=![]() =1,∴B(4,1),把B(4,1)代入y=kx﹣3得:1=4k﹣3,解得:k=1,故答案为:1,1;
=1,∴B(4,1),把B(4,1)代入y=kx﹣3得:1=4k﹣3,解得:k=1,故答案为:1,1;
(2)设C(m,m﹣3)(0<m<4),则D(m,![]() ),∴S△OCD=
),∴S△OCD=![]() =
=![]() =
=![]() ,∵0<m<4,
,∵0<m<4,![]() <0,∴当m=
<0,∴当m=![]() 时,△OCD面积取最大值,最大值为
时,△OCD面积取最大值,最大值为![]() ;
;
(3)由(1)知一次函数的解析式为y=x﹣3,由(2)知C(![]() ,﹣
,﹣![]() )、D(
)、D(![]() ,
,![]() ).
).
设C′(a,a﹣3),则O′(a﹣![]() ,a﹣
,a﹣![]() ),D′(a,a+
),D′(a,a+![]() ),∵点O′在反比例函数
),∵点O′在反比例函数![]() (x>0)的图象上,∴
(x>0)的图象上,∴![]() ,解得:a=
,解得:a=![]() 或a=﹣
或a=﹣![]() (舍去),经检验a=
(舍去),经检验a=![]() 是方程
是方程![]() 的解,∴点D′的坐标是(
的解,∴点D′的坐标是(![]() ,
,![]() ).
).



科目:初中数学 来源: 题型:
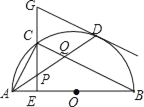
【题目】如图,在半⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQCB,其中结论正确的是____.
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQCB,其中结论正确的是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
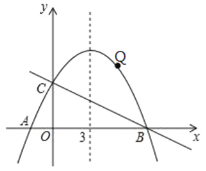
【题目】如图,已知抛物线y=ax+![]() x+4的对称轴是直线x=3,且与轴相交于A、B两点(B点在A点的右侧),与轴交于C点.
x+4的对称轴是直线x=3,且与轴相交于A、B两点(B点在A点的右侧),与轴交于C点.
(1)求出A点的坐标、B点坐标;
(2)求出直线BC的解析式;
(3)点Q是直线BC上方的抛物线上的一动点(不与B、C重合),是否存在点Q,使△QBC的面积最大.若存在,请求出△QBC的最大面积,若不存在,试说明理由;
(4)若E在x轴上,点F在抛物线上,以A、C、E、F为顶点的四边形是平行四边形时,请直接写出点E的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
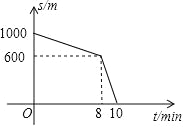
【题目】放学后,小刚和同学边聊边往家走,突然想起今天是妈妈的生日,赶紧加快速度,跑步回家.小刚离家的距离s(m)和放学后的时间t(min)之间的关系如图所示,给出下列结论:①小刚边走边聊阶段的行走速度是125m/min;②小刚家离学校的距离是1000m;③小刚回到家时已放学10min;④小刚从学校回到家的平均速度是100m/min;其中正确的个数为是( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-1,3,则下列结论正确的个数有( )①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.
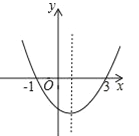
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
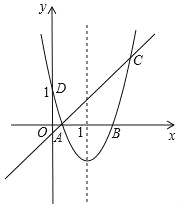
【题目】如图,一次函数y1=x﹣![]() 与x轴交点A恰好是二次函数y2与x轴的其中一个交点,已知二次函数图象的对称轴为x=1,并与y轴的交点为D(0,1).
与x轴交点A恰好是二次函数y2与x轴的其中一个交点,已知二次函数图象的对称轴为x=1,并与y轴的交点为D(0,1).
(1)求二次函数的解析式;
(2)设该二次函数与一次函数的另一个交点为C点,连接DC,求三角形ADC的面积.
(3)根据图象,直接写出当y1>y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
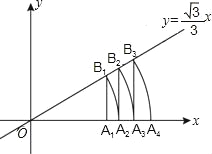
【题目】如图,直线![]() x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为______,点An______.
x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为______,点An______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com