
 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.分析 (1)根据点B的横坐标利用一次函数图象上点的坐标特征即可求出点B的坐标,根据点O的坐标结合抛物线的对称轴即可找出点A的坐标,设抛物线的函数关系式为y=ax(x-4),代入点B的坐标求出a值即可;
(2)将直线BE的函数关系式代入抛物线的函数关系式中可得出关于x的一元二次方程,由根的判别式△=0,即可得出直线BE与抛物线只有一个交点;
(3)根据点E的横坐标利用一次函数图象上点的坐标特征即可求出点E的坐标,结合点B、C的坐标利用两点间的距离公式,即可得出CE=CB,再根据点B、D、E的坐标利用两点间的距离公式,即可得出BD=DE,根据等腰三角形的三线合一即可证出CD垂直平分BE;
(4)过点E作ME⊥BE交x轴于点M,过点B作BN⊥直线x=2于点N,则△EBN∽△MEC,根据相似三角形的性质即可找出点M的坐标,由点E、M的坐标利用待定系数法可求出直线EM的函数关系式,将其代入抛物线的函数关系式中可得出关于x的一元二次方程,由根的判别式△=-60<0,即可得出直线EM与抛物线无交点,由此得出不存在满足条件的点P.
解答 解:(1)∵点B(-2,m)在直线上y=-2x-1上,
∴m=-2×(-2)-1=3,
∴B(-2,3).
∵抛物线经过原点O和点A,对称轴为x=2,
∴点A的坐标为(4,0).
设所求的抛物线对应函数关系式为y=ax(x-4),
将点B(-2,3)代入上式,
3=-2a×(-2-4),解得:a=$\frac{1}{4}$,
∴所求的抛物线对应的函数关系式为y=$\frac{1}{4}$x(x-4)=$\frac{1}{4}$x2-x.
(2)将y=-2x-1代入y=$\frac{1}{4}$x2-x,得:$\frac{1}{4}$x2-x=-2x-1,
整理得:x2+4x+4=0,
∴△=42-4×1×4=0,
∴直线BE与抛物线只有一个交点.
(3)证明:当x=2时,y=-2x-1=-5,
∴E(2,-5).
∵C(2,0),B(-2,3),
∴CE=0-(-5)=5,CB=$\sqrt{(-2-2)^{2}+(3-0)^{2}}$=5,
∴CE=CB.
∵D(0,-1),B(-2,3),E(2,-5),
∴BD=$\sqrt{(-2-0)^{2}+[3-(-1)]^{2}}$=2$\sqrt{5}$,DE=$\sqrt{(0-2)^{2}+[-1-(-5)]^{2}}$=2$\sqrt{5}$,
∴BD=DE,
∴CD垂直平分BE.
(4)不存在,理由如下: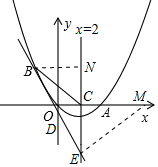
过点E作ME⊥BE交x轴于点M,过点B作BN⊥直线x=2于点N,如图所示.
∵B(-2,3),E(2,-5),
∴BN=2-(-2)=4,EN=3-(-5)=8,CE=0-(-5)=5.
∵∠BEN+∠EBN=90°,∠BEN+∠MEC=90°,
∴∠EBN=∠MEC,
∴△EBN∽△MEC,
∴$\frac{MC}{EC}=\frac{EN}{BN}$,
∴MC=10,
∴M(12,0).
设直线EM的函数关系式为y=kx+b(k≠0),
将E(2,-5)、M(12,0)代入y=kx+b,
$\left\{\begin{array}{l}{2k+b=-5}\\{12k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-6}\end{array}\right.$,
∴直线EM的函数关系式为y=$\frac{1}{2}$x-6.
将y=$\frac{1}{2}$x-6代入y=$\frac{1}{4}$x2-x,得:$\frac{1}{4}$x2-x=$\frac{1}{2}$x-6,
整理得:x2-6x+24=0,
∴△=(-6)2-4×1×24=-60<0,
∴直线EM与抛物线无交点,
∴不存在满足条件的点P.
点评 本题考查了二次函数的综合题、待定系数法求一次函数解析式、一次函数图象上点的坐标特征、根的判别式、两点间的距离公式以及等腰三角形的性质,解题的关键是:(1)根据一次函数图象上点的坐标特征找出点B的坐标;(2)由根的判别式△=0,得出直线BE与抛物线只有一个交点;(3)利用两点间的距离公式找出CE=CB、BD=DE;(4)由根的判别式△=-60<0,得出直线EM与抛物线无交点.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:填空题
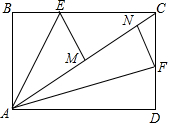 如图,矩形ABCD,将它分别沿AE和AF折叠,恰好使点B,C落到对角线AC上点M,N处,已知MN=2,NC=1,则矩形ABCD的面积是9+2$\sqrt{6}$.
如图,矩形ABCD,将它分别沿AE和AF折叠,恰好使点B,C落到对角线AC上点M,N处,已知MN=2,NC=1,则矩形ABCD的面积是9+2$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明一家人春节期间参与了“支付宝集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给其中一个,两个人各设计了一个游戏,获胜者得到“敬业福”,请用适当的方法说明这两个游戏对小明和姐姐是否公平.
小明一家人春节期间参与了“支付宝集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给其中一个,两个人各设计了一个游戏,获胜者得到“敬业福”,请用适当的方法说明这两个游戏对小明和姐姐是否公平.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
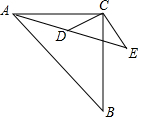 如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AE上,若AC=10,AD=2$\sqrt{10}$,求DC的长.
如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AE上,若AC=10,AD=2$\sqrt{10}$,求DC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
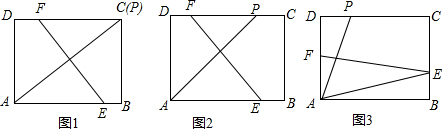
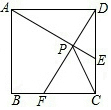 如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=2,线段CP的最小值是( )
如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=2,线段CP的最小值是( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$-1 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com