
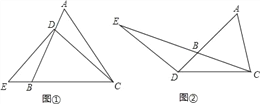
【题目】(1)已知△ABC是等腰三角形,其底边是BC,点D在线段AB上,E是直线BC上一点,且∠DEC=∠DCE,若∠A等于60°(如图①).求证:EB=AD;
(2)若将(1)中的“点D在线段AB上”改为“点D在线段AB的延长线上”,其他条件不变(如图②),(1)的结论是否成立,并说明理由。
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)作DF∥BC交AC于F,由平行线的性质得出∠ADF=∠ABC,∠AFD=∠ACB,∠FDC=∠DCE,证明△ABC是等边三角形,得出∠ABC=∠ACB=60°,证出△ADF是等边三角形,∠DFC=120°,得出AD=DF,由已知条件得出∠FDC=∠DEC,ED=CD,由AAS证明△DBE≌△CFD,得出EB=DF,即可得出结论;
(2)作DF∥BC交AC的延长线于F,同(1)证出△DBE≌△CFD,得出EB=DF,即可得出结论.
试题解析:(1)证明:如图,作DF∥BC交AC于F,
则△ADF为等边三角形
∴AD=DF,又∵ ∠DEC=∠DCB,
∠DEC+∠EDB=60°,
∠DCB+∠DCF=60° ,
∴ ∠EDB=∠DCA ,DE=CD,
在△DEB和△CDF中,
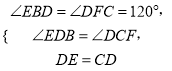
∴△DEB≌△CDF,
∴BD=DF,
∴BE=AD .
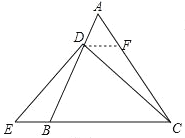
(2). EB=AD成立;
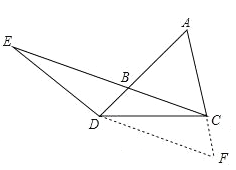
理由如下:作DF∥BC交AC的延长线于F,如图所示:
同(1)得:AD=DF,∠FDC=∠ECD,∠FDC=∠DEC,ED=CD,
又∵∠DBE=∠DFC=60°,
∴△DBE≌△CFD(AAS),
∴EB=DF,
∴EB=AD.


科目:初中数学 来源: 题型:
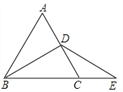
【题目】已知,如图,△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD,不添加辅助线,请你写出四个正确结论①________;②_________;③____________;④______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内任意一点P(x0 , y0),将△ABC平移后,点P的对应点为P1(x0+5,y0﹣3).
(1)写出将△ABC平移后,△ABC中A、B、C分别对应的点A1、B1、C1的坐标,并画出△A1B1C1 .
(2)若△ABC外有一点M经过同样的平移后得到点M1(5,3),写出M点的坐标,若连接线段MM1、PP1 , 则这两条线段之间的关系是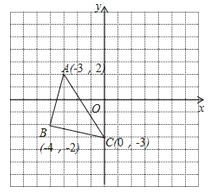
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年第九届贵阳国际汽车展览会暨新能源智能汽车展于4月18日—22日在贵阳国际会议展览中心举行,据统计,这五天共销售各种车辆约350万台,350万这个数用科学记数法表示为( )
A.3.5×105.B.35×105.C.3.5×106.D.0.35×107.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“一日捐”活动中,九(2)班42名同学捐款金额统计如下表,则在这次活动中,该班同学捐款金额的众数是( )
金额(元) | 20 | 30 | 35 | 50 | 100 | 150 |
学生数(名) | 5 | 7 | 9 | 13 | 5 | 3 |
A.3B.35C.50D.150
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是不可能事件的是( )
A.任意画一个菱形,是中心对称图形B.过平面内任意三点画一个圆
C.垂直于弦的半径平分这条弦D.半径为3的圆中有一条弦长7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com