
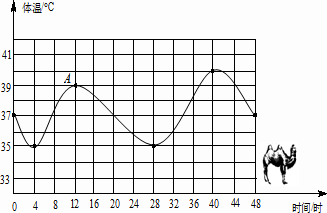
分析 (1)找到第一天中最高点与最低点的坐标,进而可得骆驼体温的变化范围与它的体温从最低上升到最高需要时间;
(2)根据图象找出第一天8时和第二天8时的温度,进行比较即可;
(3)根据横纵坐标的特点得出A点表示的意义,再找出37、44时的体温与A点所表示的体温相同.
解答 解:(1)观察图象可得,
第一天即横坐标在0到24之间,其间最高点的坐标是(12,39),最低点的坐标是(4,35);
故骆驼体温的变化范围是:35℃~40℃,
它的体温从最低上升到最高需要12-4=8小时;
(2)根据图象可知,第一天8时骆驼的体温是37.5℃,第二天8时骆驼的体温是36℃,
从而得出第一天8时比第二天8时的温度高;
(3)A点表示的是第一天12时骆驼的温度是39℃,
还有37时的体温和44时的体温与A点所表示的体温相同.
点评 本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
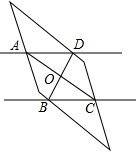 如图,一把宽为$\sqrt{3}$cm的直尺放在一个边长为2$\sqrt{3}$cm,一顶角为30°的菱形纸片上,尺子边缘与菱形纸片相交于点A,B,C,D,连接AC,BD它们相交于点O,则∠AOD的度数为75°.
如图,一把宽为$\sqrt{3}$cm的直尺放在一个边长为2$\sqrt{3}$cm,一顶角为30°的菱形纸片上,尺子边缘与菱形纸片相交于点A,B,C,D,连接AC,BD它们相交于点O,则∠AOD的度数为75°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com