
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.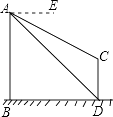
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
【答案】
(1)解:根据题意得:BD∥AE,
∴∠ADB=∠EAD=45°,
∵∠ABD=90°,
∴∠BAD=∠ADB=45°,
∴BD=AB=60,
∴两建筑物底部之间水平距离BD的长度为60米;
(2)解:延长AE、DC交于点F,
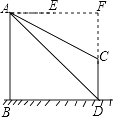
根据题意得四边形ABDF为正方形,
∴AF=BD=DF=60,
在Rt△AFC中,∠FAC=30°,
∴CF=AFtan∠FAC=60× ![]() =20
=20 ![]() ,
,
又∵FD=60,
∴CD=60﹣20 ![]() ,
,
∴建筑物CD的高度为(60﹣20 ![]() )米.
)米.
【解析】(1)根据题意得:BD∥AE,然后根据平行线的性质的出∠ADB=∠EAD=45°,从而根据三角形的内角和判断出∠BAD=∠ADB=45°,根据等腰三角形的性质得出BD=AB=60;
(2)延长AE、DC交于点F,根据正方形的性质得出AF=BD=DF=60,然后在Rt△AFC中,利用锐角三角函数的定义得出CF的长,从而得出CD的长。
【考点精析】关于本题考查的平行线的性质和等腰三角形的性质,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等腰三角形的两个底角相等(简称:等边对等角)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣3,4),B(﹣5,2),C(﹣2,1).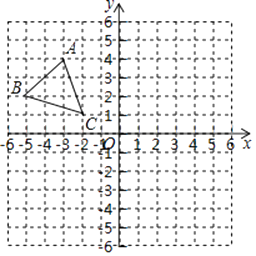
(1)画出△ABC关于y轴对称图形△A1B1C1;
(2)画出将△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2;
(3)求(2)中线段OA扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).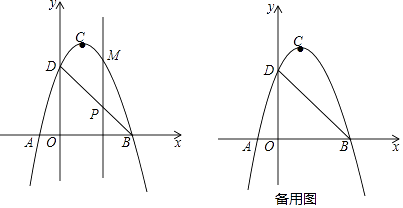
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为2 ![]() ?若存在求出点Q的坐标;若不存在请说明理由.
?若存在求出点Q的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
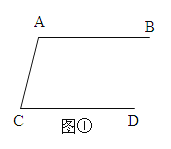
【题目】(1)如图①,AB∥CD,那么∠A+∠C= 度
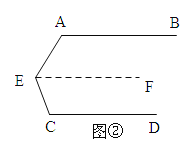
(2)如图②,AB∥CD∥EF,那么∠A+∠AEC+∠C= 度
(3)如图③,AB∥GH∥MN∥CD,那么∠A+∠AGM+∠GMC+∠C=度,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利过程.下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题: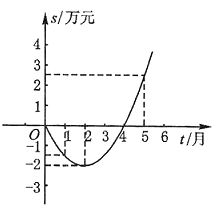
(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
(1)求购买该品牌一个台灯、一个手电筒各需要多少元?
(2)经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于被墨水污染,一道数学题仅能见到如下文字:已知二次函数y=ax2+bx+c的图象过点(1,0)… 求证:这个二次函数的图象关于直线x=2对称,根据现有信息,题中的二次函数具有的性质:
(1 )过点(3,0)
(2 )顶点是(1,﹣2)
(3 )在x轴上截得的线段的长度是2
(4 )c=3a
正确的个数( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点![]() 的坐标.
的坐标.
(1)点![]() 在
在![]() 轴上;
轴上;
(2)点![]() 的横坐标比纵坐标大2;
的横坐标比纵坐标大2;
(3)点![]() 在过
在过![]() ,且与
,且与![]() 轴平行的直线上.
轴平行的直线上.
(4)点![]() 在到两个坐标轴的距离相等.
在到两个坐标轴的距离相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com