
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).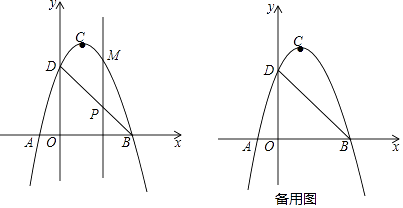
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为2 ![]() ?若存在求出点Q的坐标;若不存在请说明理由.
?若存在求出点Q的坐标;若不存在请说明理由.
【答案】
(1)
解:∵抛物线的顶点C的坐标为(1,4),
∴可设抛物线解析式为y=a(x﹣1)2+4,
∵点B(3,0)在该抛物线的图象上,
∴0=a(3﹣1)2+4,解得a=﹣1,
∴抛物线解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3,
∵点D在y轴上,令x=0可得y=3,
∴D点坐标为(0,3),
∴可设直线BD解析式为y=kx+3,
把B点坐标代入可得3k+3=0,解得k=﹣1,
∴直线BD解析式为y=﹣x+3
(2)
解:设P点横坐标为m(m>0),则P(m,﹣m+3),M(m,﹣m2+2m+3),
∴PM=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣ ![]() )2+
)2+ ![]() ,
,
∴当m= ![]() 时,PM有最大值
时,PM有最大值 ![]()
(3)
解:如图,过Q作QG∥y轴交BD于点G,交x轴于点E,作QH⊥BD于H,

设Q(x,﹣x2+2x+3),则G(x,﹣x+3),
∴QG=|﹣x2+2x+3﹣(﹣x+3)|=|﹣x2+3x|,
∵△BOD是等腰直角三角形,
∴∠DBO=45°,
∴∠HGQ=∠BGE=45°,
当△BDQ中BD边上的高为2 ![]() 时,即QH=HG=2
时,即QH=HG=2 ![]() ,
,
∴QG= ![]() ×2
×2 ![]() =4,
=4,
∴|﹣x2+3x|=4,
当﹣x2+3x=4时,△=9﹣16<0,方程无实数根,
当﹣x2+3x=﹣4时,解得x=﹣1或x=4,
∴Q(﹣1,0)或(4,﹣5),
综上可知存在满足条件的点Q,其坐标为(﹣1,0)或(4,﹣5)
【解析】(1)可设抛物线解析式为顶点式,由B点坐标可求得抛物线的解析式,则可求得D点坐标,利用待定系数法可求得直线BD解析式;(2)设出P点坐标,从而可表示出PM的长度,利用二次函数的性质可求得其最大值;(3)过Q作QG∥y轴,交BD于点G,过Q和QH⊥BD于H,可设出Q点坐标,表示出QG的长度,由条件可证得△DHG为等腰直角三角形,则可得到关于Q点坐标的方程,可求得Q点坐标.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
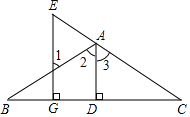
【题目】如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1,求证:AD平分∠ABC.下面是部分推理过程,请你将其补充完整:
∵AD⊥BC于D,EG⊥BC(已知)
∴∠ADC=∠EGC=90°( )
∴EG∥AD( )
∴∠E=________( )、
∠1=__________( )
又∵∠E=∠1(已知)
∴∠2=∠3( )
∴AD平分∠BAC ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间价格比淡季上涨 ![]() .下表是去年该酒店豪华间某两天的相关记录:
.下表是去年该酒店豪华间某两天的相关记录:
淡季 | 旺季 | |
未入住房间数 | 10 | 0 |
日总收入(元) | 24000 | 40000 |
(1)该酒店豪华间有多少间?旺季每间价格为多少元?
(2)今年旺季来临,豪华间的间数不变.经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间.不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图,不写作法,保留作图痕迹.
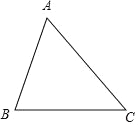
如图,△ABC中,∠A=60°.
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到AB、BC两边的距离也相等(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,若∠ACP=15°,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接食品安全检查,南通市计划对崇川区![]() 两类饭店全部进行改造.根据预算,共需资金1500万元,改造两个
两类饭店全部进行改造.根据预算,共需资金1500万元,改造两个![]() 类饭店和三个
类饭店和三个![]() 类饭店共需资金325万元;改造一个
类饭店共需资金325万元;改造一个![]() 类饭店和四个
类饭店和四个![]() 类饭店共需资金350万元.
类饭店共需资金350万元.
(1)改造一个![]() 类饭店和一个
类饭店和一个![]() 类饭店所需资金分别是多少万元?
类饭店所需资金分别是多少万元?
(2)若需改造的![]() 类饭店不超过6个,则
类饭店不超过6个,则![]() 类饭店至少有多少个?
类饭店至少有多少个?
(3)今年计划对![]() 两类饭店共7个进行改造,改造资金由市财政和区财政共同承担.若今年市财政拨付的改造资金不超过420万元;区财政投入的改造资金不少于68万元,其中区财政投入到
两类饭店共7个进行改造,改造资金由市财政和区财政共同承担.若今年市财政拨付的改造资金不超过420万元;区财政投入的改造资金不少于68万元,其中区财政投入到![]() 两类饭店的改造资金分别为每个8万元和12万元,请你通过计算求出有几种改造方案.
两类饭店的改造资金分别为每个8万元和12万元,请你通过计算求出有几种改造方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.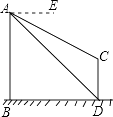
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB,OF⊥CD.
(1)若OC恰好是∠AOE的平分线,则OA是∠COF的平分线吗?请说明理由;
(2)若∠EOF=5∠BOD,求∠COE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com