Question

二次函数y=

2

3

x²的图象如图所示，点A₀位于坐标原点，A₁，A₂，A₃，…，A₂₀₁₂在y轴的正半轴上，B₁，B₂，B₃，…B₂₀₁₂在函数y=

2

3

x²第一象限的图象上，若△A₀B₁A₁，△A₁B₂A₂，△A₂B₃A₃，…，△A₂₀₁₁B₂₀₁₂A₂₀₁₂都为等边三角形，计算出△A₂₀₁₁B₂₀₁₂A₂₀₁₂的边长为

 

．

Answer 1

考点：二次函数的性质,二次函数图象上点的坐标特征,等边三角形的性质

专题：规律型

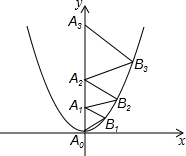
分析：根据等边三角形的性质可得∠A₁A₀B₁=60°，然后表示出A₀B₁的解析式，与二次函数解析式联立求出点B₁的坐标，再根据等边三角形的性质求出A₀A₁，同理表示出A₁B₂的解析式，与二次函数解析式联立求出点B₂的坐标，再根据等边三角形的性质求出A₁A₂，同理求出B₃的坐标，然后求出A₂A₃，从而得到等边三角形的边长为从1开始的连续自然数，与三角形所在的序数相等．

解答：解：∵△A₀B₁A₁是等边三角形，
∴∠A₁A₀B₁=60°，
∴A₀B₁的解析式为y=

3

3

x，
联立

y= 3 3 x y= 2 3 x2

，
解得

x1= 3 2 x2= 1 2

，

x2=0 y2=0

（为原点，舍去），
∴点B₁（

3

2

，

1

2

），
∴等边△A₀B₁A₁的边长为

1

2

×2=1，
同理，A₁B₂的解析式为y=

3

3

x+1，
联立

y= 3 3 x+1 y= 2 3 x2

，
解得

x1= 3 y1=2

，

x2= 3 2 y2= 1 2

（在第二象限，舍去），
∴B₂（

3

，2），
∴等边△A₁B₂A₂的边长A₁A₂=2×（2-1）=2，
同理可求出B₃（

3 3

2

，

9

2

），
所以，等边△A₂B₃A₃的边长A₂A₃=2×（

9

2

-1-2）=3，
…，
以此类推，系列等边三角形的边长为从1开始的连续自然数，
△A₂₀₁₁B₂₀₁₂A₂₀₁₂的边长A₂₀₁₁A₂₀₁₂=2012．
故答案为：2012．

点评：本题考查了二次函数图象上点的坐标特征，等边三角形的性质，主要利用了联立两函数解析式求交点坐标，根据点B系列的坐标求出等边三角形的边长并且发现系列等边三角形的边长为从1开始的连续自然数是解题的关键．