
【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:

根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
【答案】(1)70,0.2;(2)补图见解析;(3)80≤x<90;(4)750人.
【解析】
试题分析:(1)根据第一组的频数是10,频率是0.05,求得数据总数,再用数据总数乘以第四组频率可得m的值,用第三组频数除以数据总数可得n的值;
(2)根据(1)的计算结果即可补全频数分布直方图;
(3)根据中位数的定义,将这组数据按照从小到大的顺序排列后,处于中间位置的数据(或中间两数据的平均数)即为中位数;
(4)利用总数3000乘以“优”等学生的所占的频率即可.
试题解析:(1)本次调查的总人数为10÷0.05=200,
则m=200×0.35=70,n=40÷200=0.2,
(2)频数分布直方图如图所示,
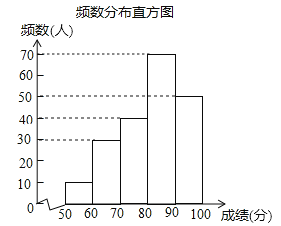
(3)200名学生成绩的中位数是第100、101个成绩的平均数,而第100、101个数均落在80≤x<90,
∴这200名学生成绩的中位数会落在80≤x<90分数段,
(4)该校参加本次比赛的3000名学生中成绩“优”等的约有:3000×0.25=750(人).


科目:初中数学 来源: 题型:
【题目】中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一副”弦图“,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1 , S2 , S3 , 若S1+S2+S3=18,则正方形EFGH的面积为 . 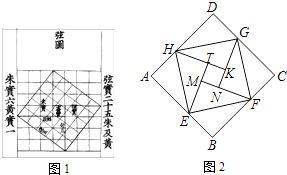
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2). 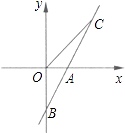
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
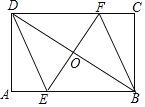
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
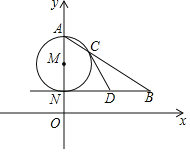
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:如图1,将三角板放在正方形ABCD上,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交边DC与点E,求证:PB=PE
分析问题:学生甲:如图1,过点P作PM⊥BC,PN⊥CD,垂足分别为M,N通过证明两三角形全等,进而证明两条线段相等.
学生乙:连接DP,如图2,很容易证明PD=PB,然后再通过“等角对等边”证明PE=PD,就可以证明PB=PE了.
解决问题:请你选择上述一种方法给予证明.
问题延伸:如图3,移动三角板,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交DC的延长线于点E,PB=PE还成立吗?若成立,请证明;若不成立,请说明理由.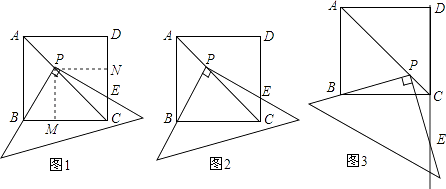
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com