
 某小区改造项目中,要将一棵没有价值的树放倒,栽上白玉兰,在操作过程中,李师傅要直接把树放倒,张师傅不同意,他担心这样会损坏这棵树周围7米处的花园和雕塑.请你根据图中标注的测量数据:∠BCD=60°,∠DCA=5°,BD=6米,通过计算说明:张师傅的担心是否有必要?(供选数据:sin65°≈0.9,cos65°≈0.4,tan65°≈2.1,
某小区改造项目中,要将一棵没有价值的树放倒,栽上白玉兰,在操作过程中,李师傅要直接把树放倒,张师傅不同意,他担心这样会损坏这棵树周围7米处的花园和雕塑.请你根据图中标注的测量数据:∠BCD=60°,∠DCA=5°,BD=6米,通过计算说明:张师傅的担心是否有必要?(供选数据:sin65°≈0.9,cos65°≈0.4,tan65°≈2.1,| 3 |
科目:初中数学 来源: 题型:
| A、三角形的三条高都在三角形的内部 |
| B、过一点有且只有一条直线与已知直线平行 |
| C、两条直线被第三条直线所截,同旁内角互补 |
| D、平移前后图形的形状和大小都没有发生改变 |
查看答案和解析>>
科目:初中数学 来源: 题型:
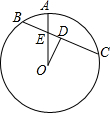 如图,D是⊙O弦BC的中点,A是
如图,D是⊙O弦BC的中点,A是 |
| BC |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,为测量一座地标性高楼的高度,小明在A点处测得楼顶D点的仰角为60°,在B点处测得楼顶D点的仰角为30°,A、B、C三点在一条直线上,已知AB=40
如图,为测量一座地标性高楼的高度,小明在A点处测得楼顶D点的仰角为60°,在B点处测得楼顶D点的仰角为30°,A、B、C三点在一条直线上,已知AB=40| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 热气球的探测器显示,从热气球A看一栋高楼顶部B处的仰角为30°,看这栋高楼底部C处的俯角为60°,若热气球与高楼的水平距离为90m,则这栋高楼有多高?(结果保留整数,
热气球的探测器显示,从热气球A看一栋高楼顶部B处的仰角为30°,看这栋高楼底部C处的俯角为60°,若热气球与高楼的水平距离为90m,则这栋高楼有多高?(结果保留整数,| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com