
【题目】如图,互相垂直的两条射线OE与OF的端点O在三角板的内部,与三角板两条直角边的交点分别为点D、B.
(1)填空:若∠ABO=50°,则∠ADO= ;
(2)若DC、BP分别是∠ADO、∠ABF的角平分线,如图1.求证:DC⊥BP;
(3)若DC、BP分别分别是∠ADE、∠ABF的角平分线,如图2.猜想DC与BP的位置关系,并说明理由.
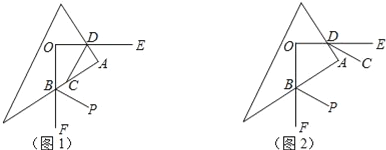
【答案】(1)130°;(2)证明见解析,(3)DC与BP互相平行.理由见解析.
【解析】试题分析:(1)由四边形的内角和为360°即可得;
(2)如图1,延长DC交BP于G,由∠OBA+∠ODA=180°、∠OBA+∠ABF=180°可得∠ODA=∠ABF,再由DC、BP分别是∠ADO、∠ABF的角平分线,从而可得∠CDA=∠CBG,再由∠DCA=∠BCG,继而可得∠BGC=∠A=90°,即得DC⊥BP;
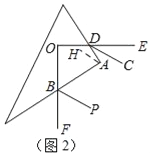
(3)DC与BP互相平行.如图2,作过点A作AH∥BP,则可得∠ABP=∠BAH,由∠OBA+∠ODA=180°,可得∠ABF+∠ADE=180°,再由DC、BP分别分别是∠ADE、∠ABF的角平分线,从而可得∠ADC+∠ABP=90°,进而可得∠DAH=∠ADC,从而可得CD∥AH,最后得CD∥BP.
试题解析:(1)如图1,∵OE⊥OF,∴∠EOF=90°,
在四边形OBAD中,∠A=∠BOD=90°,∠ABO=50°,
∴∠ADO=360°﹣90°﹣90°﹣50°=130°;
故答案为:130°;
(2)如图1,延长DC交BP于G,
∵∠OBA+∠ODA=180°,而∠OBA+∠ABF=180°,∴∠ODA=∠ABF,
∵DC、BP分别是∠ADO、∠ABF的角平分线,∴∠CDA=∠CBG,
而∠DCA=∠BCG,∴∠BGC=∠A=90°,∴DC⊥BP;

(3)DC与BP互相平行.
理由:如图2,作过点A作AH∥BP,则∠ABP=∠BAH,
∵∠OBA+∠ODA=180°,∴∠ABF+∠ADE=180°,
∵DC、BP分别分别是∠ADE、∠ABF的角平分线,∴∠ADC+∠ABP=90°,
∴∠ADC+∠BAH=90°,
而∠DAH+∠BAH=90°,∴∠DAH=∠ADC,∴CD∥AH,∴CD∥BP.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
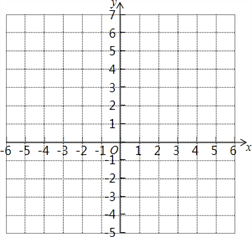
【题目】在如图所示的平面直角坐标系中表示下面各点:
A(2,0);B(1,-3);C(3,-5); D(-3,-5);E(3,5);F(5,7).
(1)A点到原点O的距离是 ______ .
(2)将点C向x轴的负方向平移6个单位,它与点 ______ 重合.
(3)连接CE,则直线CE与x轴,y轴分别是什么关系?
(4)点F到x、y轴的距离分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题:
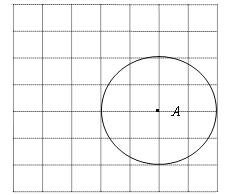
(1)根据A点坐标建立平面直角坐标系;
(2)将⊙A向左平移____________个单位长度与y轴首次相切,得到⊙A,并画出⊙A.此时点A的坐标为_____________.
(3)求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为: ;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 检测我市正在销售的酸奶的质量,应该采用抽样调查的方式
B. 在连续5次数学周考测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定
C. 某同学连续10次投掷质量均匀的硬币,3次正面向上,因此正面向上的概率是30%
D. “打开电视机,正在播放少儿节目”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣(﹣2)+(﹣3); (2)(﹣7)×(﹣![]() );
);
(3)﹣![]() ÷(﹣7)×(+2
÷(﹣7)×(+2![]() ) ; (4)23﹣6×(﹣3)+2×(﹣4) ;
) ; (4)23﹣6×(﹣3)+2×(﹣4) ;
(5) (﹣5.3)+|﹣2.5|+(﹣3.2)﹣(+4.8); (6) ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”,若“关联数”[1,m﹣2]的一次函数是正比例函数,则关于x的方程x2+3x+m=0的解为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
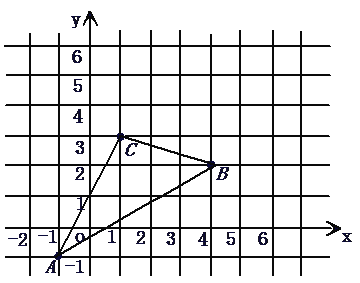
(1)请写出△ABC各点的坐标.
(2)求出S△ABC.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知□ABCD中,直线m绕点A旋转,直线m不经过B、C、D点,过B、C、D分别作BE⊥m于E, CF⊥m于F, DG⊥m于G.
(1)当直线m旋转到如图1位置时,线段BE、CF、DG之间的数量关系是 _;
(2)当直线m旋转到如图2位置时,线段BE、CF、DG之间的数量关系是 _;
(3)当直线m旋转到如图3的位置时,线段BE、CF、DG之间有怎样的数量关系?请直接写出你的猜想,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com