
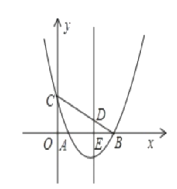
【题目】如图所示,已知抛物线![]() 与x 轴交于A ,B 两点,与y 轴交于点C ,点B 的坐标为(3,0) ,抛物线的对称轴x=2 交x 轴于点E .
与x 轴交于A ,B 两点,与y 轴交于点C ,点B 的坐标为(3,0) ,抛物线的对称轴x=2 交x 轴于点E .
(1) 求交点A 的坐标及抛物线的函数关系式;
(2) 在平面直角坐标系xOy 中是否存在点P ,使点P 与A ,B ,C 三点构成一个平行四边形?若存在,请直接写出点P 坐标:若不存在,请说明理由;
(3) 连接CB 交抛物线对称轴于点D ,在抛物线上是否存在一点Q ,使得直线CQ 把四边形 分成面积比为1:7 的两部分?若存在,请求出点Q 坐标;若不存在,请说明理由.
【答案】(1)A (1,0),y=x![]() -4x+3(2)存在,理由见解析(3)存在,(-5,48),(
-4x+3(2)存在,理由见解析(3)存在,(-5,48),(![]() )
)
【解析】
(1)把点B的坐标为(3,0)代入抛物线![]() 得到b,c的关系式;又因为抛物线的对称轴x=2,可求出b的值,进而求出求交点A的坐标及抛物线的函数关系式;
得到b,c的关系式;又因为抛物线的对称轴x=2,可求出b的值,进而求出求交点A的坐标及抛物线的函数关系式;
(2)分别以AC,AB为对角线各可求得一点再以AC,AB为边求得一点;
(3)此小题要分类讨论当分的图象左边部分是三角形右边部分是四边形或当分的图象左边部分是四边形右边部分是三角形时分别计算满足题意的Q值即可
(1)抛物线![]() 与x轴交点B(3,0)对称轴x=2
与x轴交点B(3,0)对称轴x=2
∴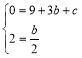
解得![]()
∴抛物线的函数关系式为y=x![]() -4x+3,
-4x+3,
令y=0,则x![]() -4x+3=0
-4x+3=0
解得x![]() =1,x
=1,x![]() =3
=3
∴抛物线与x轴另一个交点A的坐标(1,0);
(2)存在,
满足条件的点P有3个,分别为(-2,3),(2,3)(4,-3).
(3)存在,
①当分的图象左边部分是三角形右边部分是四边形
当x=0时,y=x![]() -4x+3=3,
-4x+3=3,
∴点C的坐标为(0,3),
过点CN的直线关系式y=9x+3
∴![]()
解得![]()
∴Q(-5,48);
②当分的图象左边部分是四边形右边部分是三角形时,
过点CN的直线关系式y=![]() x+3,
x+3,
∴![]()
∴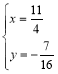
∴Q(![]() )
)
综上所述符合条件的Q有两个坐标别是(-5,48); (![]() )
)


科目:初中数学 来源: 题型:
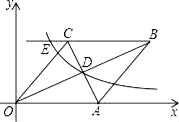
【题目】如图,已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=![]() (x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
(x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
①双曲线的解析式为y=![]() (x>0);
(x>0);
②E点的坐标是(5,8);
③sin∠COA=![]() ;
;
④AC+OB=12![]() .
.
其中正确的结论有 (填上序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好数学的甲、乙两个同学做了一个数字游戏:拿出三张正面写有数字﹣1,0,1且背面完全相同的卡片,将这三张卡片背面朝上洗匀后,甲先随机抽取一张,将所得数字作为p的值,然后将卡片放回并洗匀,乙再从这三张卡片中随机抽取一张,将所得数字作为q值,两次结果记为![]() .
.
(1)请你帮他们用树状图或列表法表示![]() 所有可能出现的结果;
所有可能出现的结果;
(2)求满足关于x的方程![]() 没有实数根的概率.
没有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
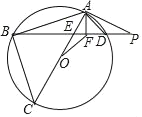
【题目】如图,△ABC内接于半径为![]() 的⊙O,AC为直径,AB=
的⊙O,AC为直径,AB=![]() ,弦BD与AC交于点E,点P为BD延长线上一点,且∠PAD=∠ABD,过点A作AF⊥BD于点F,连接OF.
,弦BD与AC交于点E,点P为BD延长线上一点,且∠PAD=∠ABD,过点A作AF⊥BD于点F,连接OF.
(1)求证:AP是⊙O的切线;
(2)求证:∠AOF=∠PAD;
(3)若tan∠PAD=![]() ,求OF的长.
,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
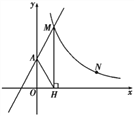
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)在y轴上是否存在点B,使以点B、A、H、M为顶点的四边形是平行四边形?如果存在,求出B点坐标;如果不存在,请说明理由;
(3)点N(a,1)是反比例函数y=![]() (x>0)图象上的点,在x轴上有一点P,使得PM+PN最小,请求出点P的坐标.
(x>0)图象上的点,在x轴上有一点P,使得PM+PN最小,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ACE中,∠AEC=90°,CB平分∠ACE交AE于点B,AC边上一点O,⊙O经过点B、C,与AC交于点D,与CE交于点F,连结BF。
(1)求证:AE是⊙O的切线;
(2)若![]() ,AE=8,求⊙O的半径;
,AE=8,求⊙O的半径;
(3)在(2)条件下,求BF的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com