
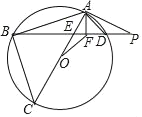
【题目】如图,△ABC内接于半径为![]() 的⊙O,AC为直径,AB=
的⊙O,AC为直径,AB=![]() ,弦BD与AC交于点E,点P为BD延长线上一点,且∠PAD=∠ABD,过点A作AF⊥BD于点F,连接OF.
,弦BD与AC交于点E,点P为BD延长线上一点,且∠PAD=∠ABD,过点A作AF⊥BD于点F,连接OF.
(1)求证:AP是⊙O的切线;
(2)求证:∠AOF=∠PAD;
(3)若tan∠PAD=![]() ,求OF的长.
,求OF的长.
【答案】(1)证明见解析(2)见解析(3)![]()
【解析】
(1)根据圆周角定理得到∠ABC=90°,推出PA⊥AC,于是得到AP是⊙O的切线;
(2)解直角三角形得到∠C=45°,求得FA=FD,连接OD,根据全等三角形的性质得到∠AOF=∠DOF,于是得到结论;
(3)延长OF交AD于点G,根据等腰三角形的性质得到OG⊥AD,解直角三角形即可得到结论.
(1)证明:∵AC是⊙O的直径,
∴∠ABC=90°,
即∠ABD+∠CBD=90°,
∵![]() ,
,
∴∠CAD=∠CBD,
∵∠PAD=∠ABD,
∴∠PAD+∠CAD=∠ABD+∠CBD=90°,
即PA⊥AC,
∵AC是⊙O的直径,
∴AP是⊙O的切线;
(2)解:∵在Rt△ABC中,![]() ,
,
∴sinC=![]() ,
,
∴∠C=45°,
∵![]() ,
,
∴∠ADB=∠C=45°,
∵AF⊥BD,
∴∠FAD=∠ADB=45°,
∴FA=FD,
连接OD,
∵OA=OD,OF=OF,FA=FD,
∴△AOF≌△DOF(SSS),
∴∠AOF=∠DOF,
∴∠AOD=2∠AOF,
∵![]() ,
,
∴∠AOD=2∠ABD,
∴∠AOF=∠ABD,
∵∠ABD=∠PAD,
∴∠AOF=∠PAD;
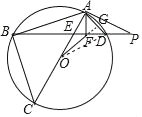
(3)解:延长OF交AD于点G,
∵OA=OD,∠AOG=∠DOG,
∴OG⊥AD,
∵tan∠PAD=![]() ,∠AOF=∠PAD,
,∠AOF=∠PAD,
∴tan∠AOF=![]() ,
,
在Rt△AOG中,AO=![]() ,
,
设AG=x,
∴AG2+OG2=AO2,
x2+(3x)2=(![]() )2,
)2,
解得:x=![]() ,
,
∴AG=![]() ,OG=
,OG=![]() ,
,
∵∠FAD=45°,OG⊥AD,
∴∠AFG=∠FAD=45°,
∴FG=AG=![]() ,
,
∴OF=OG﹣FG=![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
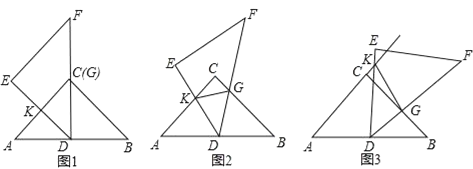
【题目】数学活动课上,小颖同学用两块完全一样的透明等腰直角三角板ABC、DEF进行探究活动.
操作:使点D落在线段AB的中点处并使DF过点C(如图1),然后将其绕点D顺时针旋转,直至点E落在AC的延长线上时结束操作,在此过程中,线段DE与AC或其延长线交于点K,线段BC与DF相交于点G(如图2,3).
探究1:在图2中,求证:△ADK∽△BGD.
探究2:在图2中,求证:KD平分∠AKG.
探究3:
①在图3中,KD仍平分∠AKG吗?若平分,请加以证明;若不平分,请说明理由.
②在以上操作过程中,若设AC=BC=8,KG=x,△DKG的面积为y,请求出y与x的函数关系式,并直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
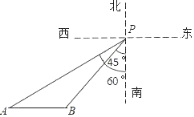
【题目】在某海域,一艘海监船在P处检测到南偏西45°方向的B处有一艘不明船只,正沿正西方向航行,海监船立即沿南偏西60°方向以40海里/小时的速度去截获不明船只,经过1.5小时,刚好在A处截获不明船只,求不明船只的航行速度.(![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留一位小数).
≈1.73,结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
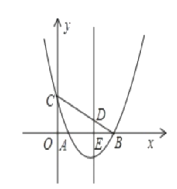
【题目】如图所示,已知抛物线![]() 与x 轴交于A ,B 两点,与y 轴交于点C ,点B 的坐标为(3,0) ,抛物线的对称轴x=2 交x 轴于点E .
与x 轴交于A ,B 两点,与y 轴交于点C ,点B 的坐标为(3,0) ,抛物线的对称轴x=2 交x 轴于点E .
(1) 求交点A 的坐标及抛物线的函数关系式;
(2) 在平面直角坐标系xOy 中是否存在点P ,使点P 与A ,B ,C 三点构成一个平行四边形?若存在,请直接写出点P 坐标:若不存在,请说明理由;
(3) 连接CB 交抛物线对称轴于点D ,在抛物线上是否存在一点Q ,使得直线CQ 把四边形 分成面积比为1:7 的两部分?若存在,请求出点Q 坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙![]() 的直径,过点A作⊙
的直径,过点A作⊙![]() 的切线并在其上取一点C,连接OC交⊙
的切线并在其上取一点C,连接OC交⊙![]() 于点D,BD的延长线交AC于E,连接AD.
于点D,BD的延长线交AC于E,连接AD.
(1)求证:![]() ;
;
(2)若AB=2,![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019中国北京世界园艺博览会于2019年4月29日至10月7日在北京市延庆区举办,预售期门票价然有“平日票”和“推定日票”两种,其中平日票的单价比指定日票的单价少40元1张:某学校计划组织学生去参观,用9600元购买的平日票的票数与用12800元购买的旅定日票的票数相等.
(1)求该学校购买的平日票、指定日票的单价分别是多少元?
(2)若两种票共购买了200张,且购买的总费用是28800元,求购买了多少张平日票?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=x+1的图象l与y轴交于点C,A1的坐标为(1,0),点B1在直线l上,且A1B1平行于y轴,连接CA1、OB1交于点P1,过点A1作A1B2∥OB1交直线l于点B2,过点B1作B1A2∥CA1交x轴于点A2,A1B2与B1A2交于点P2,……,按此进行下去,则点P2019的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了考察九年级学生的中考体育测试成绩(满分30分),随机抽查了40名学生的成绩(单位:分),得到如下的统计图①和图②.请根据相关信息,解答下列问题:
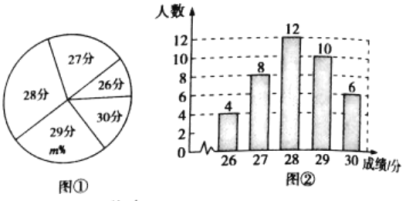
(1)图中m的值为_______________.
(2)求这40个样本数据的平均数、众数和中位数:
(3)根据样本数据,估计该中学九年级2000名学生中,体育测试成绩得满分的大约有多少名学生。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com