
【题目】如图,AB是⊙![]() 的直径,过点A作⊙
的直径,过点A作⊙![]() 的切线并在其上取一点C,连接OC交⊙
的切线并在其上取一点C,连接OC交⊙![]() 于点D,BD的延长线交AC于E,连接AD.
于点D,BD的延长线交AC于E,连接AD.
(1)求证:![]() ;
;
(2)若AB=2,![]() ,求AE的长.
,求AE的长.

【答案】(1)证明见解析;(2)![]()
【解析】
(1)由AB是⊙O的直径,AC为⊙![]() 切线得到∠ADB=∠BAE=90°,进而可知 ∠DAE+∠BAD=∠CDE+∠ODA=
切线得到∠ADB=∠BAE=90°,进而可知 ∠DAE+∠BAD=∠CDE+∠ODA=![]() ,由OA=OD可知∠OAD=∠ODA,进而可知∠BAE=∠CDE,∠C为公共角,即可证明△CDE∽△CAD,(2)根据勾股定理可求出OC的长,进而求出DC的长,通过△CDE∽△CAD即可求出AE的长.
,由OA=OD可知∠OAD=∠ODA,进而可知∠BAE=∠CDE,∠C为公共角,即可证明△CDE∽△CAD,(2)根据勾股定理可求出OC的长,进而求出DC的长,通过△CDE∽△CAD即可求出AE的长.
(1)∵AB为直径,AC为⊙![]() 切线,
切线,
∴∠ADB=∠BAE=![]() ,
,
∴∠DAE+∠BAD=∠CDE+∠ODA=![]() ,
,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠BAE=∠CDE,
∵∠C为公共角,
∴△CDE∽△CAD,
(2)∵AB=2,
∴AO=OD=1,
∵AC=![]() ,∠BAC=Rt∠,
,∠BAC=Rt∠,
∴![]() ,
,
∴DC=OC-OD=2,
∵△CDE∽△CAD,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某玩具厂工人的工作时间:每月25天,每天8小时.待遇:按件计酬.多劳多得,每月另加福利工资100元,按月结算.该厂生产A,B两种产品,工人每生产一件A产品,可得报酬![]() 元,每生产一件B产品,可得报酬
元,每生产一件B产品,可得报酬![]() 元.下表记录的是工人小李的工作情况:
元.下表记录的是工人小李的工作情况:
生产A产品的数量 | 生产B声品的数量 | 总时间 |
1 | 1 | 35 |
3 | 2 | 85 |
根据上表提供的信息,请回答下列问题:
![]() 小李每生产一件A产品、每生产一件B产品,分别需要多少分钟?
小李每生产一件A产品、每生产一件B产品,分别需要多少分钟?
![]() 设小李某月生产A产品x件,该月工资为y元,求y与x的函数表达式.
设小李某月生产A产品x件,该月工资为y元,求y与x的函数表达式.
![]() 如果生产各种产品的数目没有限制,那么小李该月的工资最多为多少?
如果生产各种产品的数目没有限制,那么小李该月的工资最多为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,图象与
,图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.

![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 设抛物线对称轴与直线
设抛物线对称轴与直线![]() 交于点
交于点![]() ,连接
,连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
![]() 点
点![]() 为直线
为直线![]() 上的任意一点,过点
上的任意一点,过点![]() 作
作![]() 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点![]() ,问是否存在点
,问是否存在点![]() 使
使![]() 为直角三角形?若存在,求出点
为直角三角形?若存在,求出点![]() 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题.
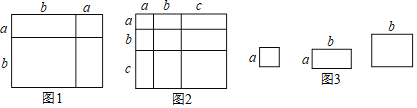
(1)写出图2中所表示的数学等式 ;
(2)根据整式乘法的运算法则,通过计算验证上述等式;
(3)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,求a2+b2+c2;
(4)利用(1)中得到的结论,直接写出代数式![]() 展开之后的结果:
展开之后的结果:![]() =
=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AB=6cm,AC=8cm,动点P以3cm/s从点B出发向终点C运动;动点Q以1cm/s从点C出发向终点B运动,动点P,Q同时出发,以PQ为直径在BC上方作半圆O,设运动时间为t(s).
(1)当t=1时,半圆O的半径R=_______;
(2)当半圆O落在△ABC的内部(包括边界)时,求t的取值范围;
(3)当点P在Q的左边时,过点P作PE//AB交半圆于点E.,求tan∠EAC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,梯形ABCD中,AB//CD,且AB=2CD,E,F分别是AB,BC的中点.
EF与BD相交于点M.

(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】传统节日“端午节”的早晨,小文妈妈为小文准备了四个粽子作早点:一个枣馅粽,一个肉馅粽,两个花生馅粽,四个粽子除内部馅料不同外,其它一切均相同.
(1)小文吃前两个粽子刚好都是花生馅粽的概率为 ;
(2)若妈妈在早点中给小文再增加一个花生馅的粽子,则小文吃前两个粽子都是花生馅粽的可能性是否会增大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角三角形ABC中,AH是BC边上的高,分别以AB,AC为一边,向外作正方形ABDE和ACFG,连接CE,BG和EG,EG与HA的延长线交于点M,下列结论:①BG=CE;②BG⊥CE;③AM是△AEG的中线;④∠EAM=∠ABC,其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com