
【题目】在Rt△ABC中,AB=6cm,AC=8cm,动点P以3cm/s从点B出发向终点C运动;动点Q以1cm/s从点C出发向终点B运动,动点P,Q同时出发,以PQ为直径在BC上方作半圆O,设运动时间为t(s).
(1)当t=1时,半圆O的半径R=_______;
(2)当半圆O落在△ABC的内部(包括边界)时,求t的取值范围;
(3)当点P在Q的左边时,过点P作PE//AB交半圆于点E.,求tan∠EAC的值.

【答案】(1)3;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)根据题意求出BP、QC的长即可.(2)分类讨论:①当点P在点Q的左侧且半圆O与边AC相切时,可证明△ODC∽△BAC,可知![]() ,根据BP=3t,CQ=t,代入求出t的值即可.;②当点P在点Q的右侧,且半圆O与边AC相切时,同理可证△ODC∽△BAC,PQ=4t-10,可求出CP=10-3t,CO=5-t根据相似三角形各边的比例关系求出t即可.结合两点求出t的取值范围即可.(3)由PE//AB可知△PFC∽△BAC,∠AFP=∠AFC=90°,得
,根据BP=3t,CQ=t,代入求出t的值即可.;②当点P在点Q的右侧,且半圆O与边AC相切时,同理可证△ODC∽△BAC,PQ=4t-10,可求出CP=10-3t,CO=5-t根据相似三角形各边的比例关系求出t即可.结合两点求出t的取值范围即可.(3)由PE//AB可知△PFC∽△BAC,∠AFP=∠AFC=90°,得![]() ,可求出PF、CF的值,进而求出AF的长,连接EQ,同理可求长PE的长,进而求出EF的长,根据正切定义求出tan∠EAC的值即可.
,可求出PF、CF的值,进而求出AF的长,连接EQ,同理可求长PE的长,进而求出EF的长,根据正切定义求出tan∠EAC的值即可.
(1)∵t=1,
∴BP=3,QC=1,
∴PQ=6,R=3.
(2)①当点P在点Q的左侧且半圆O与边AC相切时,
记切点为D,即OD⊥AC
∵∠BAC=Rt∠
∴OD//AB
∴△ODC∽△BAC
∴![]()
∵BP=3t,CQ=t ∴PQ=10-4t即OD=PO=OQ=5-2t
∴CO=5-t
∴![]() ∴
∴![]()

②当点P在点Q的右侧,且半圆O与边AC相切时,
同理得,△ODC∽△BAC,
∴![]()
∵BP=3t,CQ=t ∴PQ=4t-10即OD=PO=OQ=2t-5
∵CP=10-3t
∴CO=5-t
∴![]() ∴
∴![]()

∴![]()
(3)如图所示,PE//AB交AC于点F,连接AE
∴△PFC∽△BAC,∠BAC=∠AFC=90°
∴![]()
∵CP=10-3t
∴![]()
∴![]() ,
,![]()
∴![]()
连接EQ,得∠PEQ=∠PFC=90°
∴EQ//AC
∴△PEQ∽△PFC
同理得![]()
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】如图①,在等边三角形ABC中.D是AB边上的动点,以CD为一边,向上作等边三角形EDC.连接AE.
(l)求证:△DBC≌△EAC
(2)试说明AE∥BC的理由.
(3)如图②,当图①中动点D运动到边BA的延长线上时,所作仍为等边三角形,猜想是否仍有AE∥BC?若成立请证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
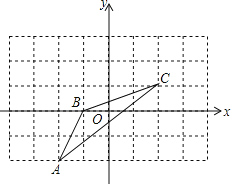
【题目】如图:
(1)作出与△ABC关于x轴对称的图形△A1B1C1;
(2)若图中一个小正方形边长为一个单位长度,请写出各点的坐标:
A1 ;B1 ;C1 ;
(3)求△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师给学生出了一道题:求(2a+b)(2a﹣b)+2(2a﹣b)2+(2ab2﹣16a2b)÷(﹣2a)的值,其中a=![]() ,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”你认为他们谁说的有道理?为什么?
,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”你认为他们谁说的有道理?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙![]() 的直径,过点A作⊙
的直径,过点A作⊙![]() 的切线并在其上取一点C,连接OC交⊙
的切线并在其上取一点C,连接OC交⊙![]() 于点D,BD的延长线交AC于E,连接AD.
于点D,BD的延长线交AC于E,连接AD.
(1)求证:![]() ;
;
(2)若AB=2,![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向A以1cm/s的速度移动.如果P、Q同时出发,用t秒表示移动的时间(0≤t≤6)那么:
(1)当t为何值时,△QAP为等腰直角三角形?
(2)对四边形QAPC的面积,提出一个与计算结果有关的结论;
(3)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 坐标为
坐标为![]() ,点
,点![]() 是
是![]() 轴正半轴上一点,且
轴正半轴上一点,且![]() ,点
,点![]() 是
是![]() 轴上位于点
轴上位于点![]() 右侧的一个动点,设点
右侧的一个动点,设点![]() 的坐标为
的坐标为![]() .
.
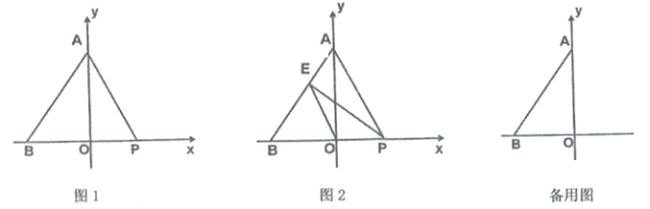
(1)点![]() 的坐标为( );
的坐标为( );
(2)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 点的坐标;
点的坐标;
(3)如图2,过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() ,连接
,连接![]() ,若点
,若点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,当点
,当点![]() 恰好落在直线
恰好落在直线![]() 上时,
上时,![]() .(直接写出答案)
.(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com