
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题.
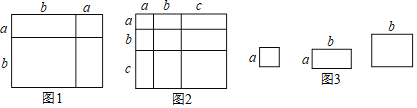
(1)写出图2中所表示的数学等式 ;
(2)根据整式乘法的运算法则,通过计算验证上述等式;
(3)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,求a2+b2+c2;
(4)利用(1)中得到的结论,直接写出代数式![]() 展开之后的结果:
展开之后的结果:![]() =
=
【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac(2)验证见解析;(3)30;(4)![]()
【解析】
(1)由大正方形等于9个长方形面积的和;
(2)根据乘法法则把(a+b+c)2计算即可;
(3)将所求式子转化为a2+b2+c2=(a+b+c)2-(2ab+2bc+2ac),代入已知条件即可;
(4)根据(1)中结论计算即可.
解:(1)∵边长为(a+b+c)的正方形的面积为:(a+b+c)2,
分部分来看的面积为a2+b2+c2+2ab+2bc+2ac,
两部分面积相等.
故答案为:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)∵(a+b+c)2
=(a+b+c)(a+b+c)
=a2+ab+ac+ab+b2+bc+ac+bc+c2
=a2+b2+c2+2ab+2bc+2ac;
(3)∵a+b+c=10,ab+ac+bc=35,
∴a2+b2+c2=(a+b+c)2﹣2ab﹣2bc﹣2ac
=102﹣2×35
=30,
∴a2+b2+c2的值为30.
(4) ![]() =
= ![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() ,现把一块直径为
,现把一块直径为![]() 的量角器(圆心为
的量角器(圆心为![]() )放置在图形上,使其
)放置在图形上,使其![]() 线
线![]() 与
与![]() 重合;若将量角器
重合;若将量角器![]() 线上的端点
线上的端点![]() 固定在点
固定在点![]() 上,再把量角器绕点
上,再把量角器绕点![]() 顺时针方向旋转
顺时针方向旋转![]() ,此时量角器的半圆弧与
,此时量角器的半圆弧与![]() 相交于点
相交于点![]() ,设点
,设点![]() 处量角器的读数为
处量角器的读数为![]() .
.

![]() 用含
用含![]() 的代数式表示
的代数式表示![]() 的大小;
的大小;
![]() 当
当![]() 等于多少时,线段
等于多少时,线段![]() 与
与![]() 平行?
平行?
![]() 在量角器的旋转过程中,过点
在量角器的旋转过程中,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .设
.设![]() ,
,![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示:

(1)根据图示填写下表:
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 |
|
|
高中部 | 85 |
|
|
(2)结合两队成绩的平均数中中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手的成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、点B是双曲线![]() 图象上的两点(A在B的右侧).延长AB交y轴正半轴于C,OC的中点为D.连结AO,BO,交点为E.若△BEO的面积为4,四边形AEDC的面积等于△BEO的面积,则k的值为_______.
图象上的两点(A在B的右侧).延长AB交y轴正半轴于C,OC的中点为D.连结AO,BO,交点为E.若△BEO的面积为4,四边形AEDC的面积等于△BEO的面积,则k的值为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙![]() 的直径,过点A作⊙
的直径,过点A作⊙![]() 的切线并在其上取一点C,连接OC交⊙
的切线并在其上取一点C,连接OC交⊙![]() 于点D,BD的延长线交AC于E,连接AD.
于点D,BD的延长线交AC于E,连接AD.
(1)求证:![]() ;
;
(2)若AB=2,![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从甲、乙两养殖场调运鸡蛋到该超市的路程和运费如下表:
到超市的路程(千米) | 运费(元/斤·千米) | |
甲养殖场 | 200 | 0.012 |
乙养殖场 | 140 | 0.015 |
设从甲养殖场调运鸡蛋x斤,总运费为W元
(1)试写出W与x的函数关系式.
(2)怎样安排调运方案才能使每天的总运费最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB与y轴交于D点,∠CAO=90°﹣∠BDO.
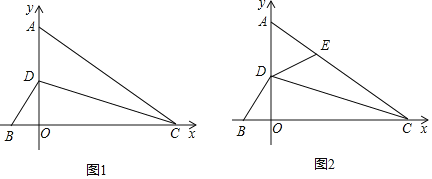
(1)求证:AC=BC;
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com